Applet: Distance from point to plane
Applet loading
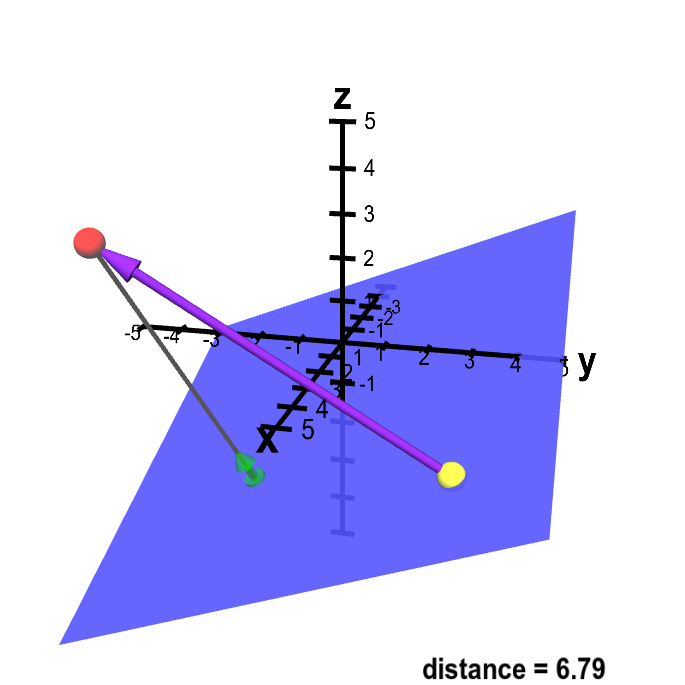
A sketch of a way to calculate the distance from point $\color{red}{P}$ (in red) to the plane. The vector $\color{green}{\vc{n}}$ (in green) is a unit normal vector to the plane. You can drag point $\color{red}{P}$ as well as a second point $\vc{Q}$ (in yellow) which is confined to be in the plane. Although the vector $\color{green}{\vc{n}}$ does not change (as the plane is fixed), it moves with $\color{red}{P}$ to always be at the end of a gray line segment from $\color{red}{P}$ that is perpendicular to the plane. This distance from $\color{red}{P}$ to the plane is the length of this gray line segment. This distance is the length of the projection of the vector from $Q$ to $P$ (in purple) onto the normal vector $\color{green}{\vc{n}}$.
Applet links
This applet is found in the pages
General information about three.js applets
The applet was made using three.js and requires Javascript as well as a browser that supports WebGL. For most three.js applets, you can drag with the mouse to rotate the view, drag with the right button to pan, and zoom in/out with the mouse wheel. Many applets contain points that you can drag to change values of variables.