Applet: Gradient and directional derivative on a mountain shown as level curves
Applet loading
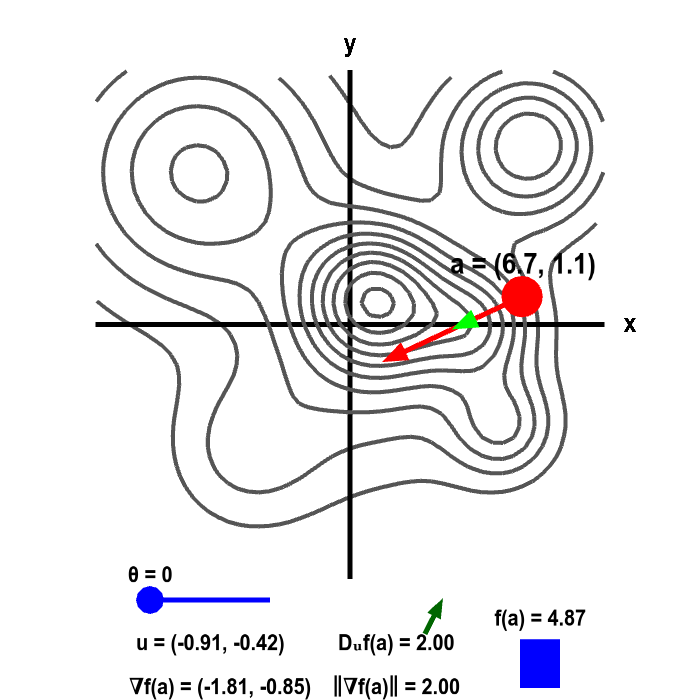
The height of a mountain ranged described by a function $f(x,y)$ is shown as a level curve plot. A point $\vc{a}$ (in red) can be moved with the mouse. The height $f(\vc{a})$ is illustrated by the bar in the lower right corner. The direction of steepest increase of $f$ is given by the gradient vector $\nabla f(\vc{a})$ (illustrated by the red vector emanating from $\vc{a}$). The actual length of the gradient $\| \nabla f(\vc{a})\|$ is indicated at the bottom, which is compared to the value of the directional derivative $D_{\vc{u}}f(\vc{a})$, where $\vc{u}$ is represented by the light green vector. The direction of $\vc{u}$ is controlled by $\theta$ (changed via slider), where $\theta$ is the angle between $\nabla f(\vc{a})$ and $\vc{u}$. The directional derivative is the slope of $f(x,y)$ in the direction $\vc{u}$, which is illustrated by the slope of the green arrow above the value of $D_{\vc{u}}f(\vc{a})$.
Applet links
General information about three.js applets
The applet was made using three.js and requires Javascript as well as a browser that supports WebGL. For most three.js applets, you can drag with the mouse to rotate the view, drag with the right button to pan, and zoom in/out with the mouse wheel. Many applets contain points that you can drag to change values of variables.