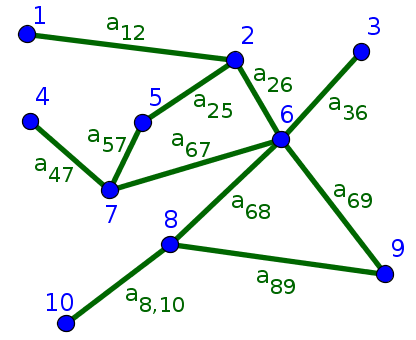
Node degree definition
The degree of a node is the number of edges connected to the node. In terms of the adjacency matrix $A$, the degree for a node indexed by $i$ in an undirected network is \begin{gather*} k_i=\sum_j a_{ij}, \end{gather*} where the sum is over all nodes in the network.
In a directed network, each node has two degrees. The out-degree is the number of outgoing edges emanating from a node \begin{gather*} k_i^{\text{out}}=\sum_j a_{ji}, \end{gather*} and the in-degree is the number of incoming edges onto a node \begin{gather*} k_i^{\text{in}}=\sum_j a_{ij}. \end{gather*} The total degree of the node is the sum of its in- and out-degree \begin{gather*} k_i^{\text{tot}} = k_i^{\text{in}} + k_i^{\text{out}}. \end{gather*}
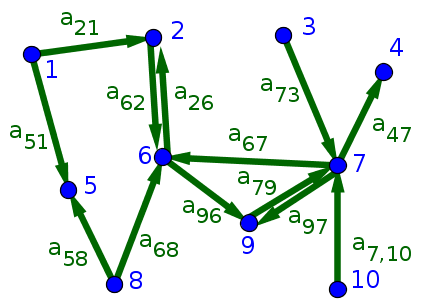
For this directed network, the degrees are $k_1^{\text{in}}=0$, $k_1^{\text{out}}=2$, $k_1^{\text{tot}}=2$, $k_2^{\text{in}}=2$, $k_2^{\text{out}}=1$, $k_2^{\text{tot}}=3$, $k_3^{\text{in}}=0$, $k_3^{\text{out}}=1$, $k_3^{\text{tot}}=1$, $k_4^{\text{in}}=1$, $k_4^{\text{out}}=0$, $k_4^{\text{tot}}=1$, $k_5^{\text{in}}=2$, $k_5^{\text{out}}=0$, $k_5^{\text{tot}}=2$, $k_6^{\text{in}}=3$, $k_6^{\text{out}}=2$, $k_6^{\text{tot}}=5$, $k_7^{\text{in}}=3$, $k_7^{\text{out}}=3$, $k_7^{\text{tot}}=6$, $k_8^{\text{in}}=0$, $k_8^{\text{out}}=2$, $k_8^{\text{tot}}=2$, $k_9^{\text{in}}=2$, $k_9^{\text{out}}=1$, $k_9^{\text{tot}}=3$, $k_{10}^{\text{in}}=0$, $k_{10}^{\text{out}}=1$, $k_{10}^{\text{tot}}=1$.
For more information about networks, see the network introduction.