Math Insight

Solutions to elementary discrete dynamical systems biology problems, part 2

Problem 1

1. The dynamical system is already in the form $x_{n+1}=f(x_n)$ where $f(x)=5xe^{-x}$. The derivative is \begin{align*} f'(x) &= 5e^{-x} -5xe^{-x}\\ &= 5(1-x)e^{-x}. \end{align*} Since $f'(0)=5e^0 = 5 > 1$, the equilibrium $x_n=0$ is unstable. Since \begin{align*} f'(\ln(5)) &= 5(1-\ln(5))e^{-\ln(5)}\\ &= 5(1-\ln(5))e^{\ln(1/5)}\\ &= 5(1-\ln(5))/5\\ &= 1-\ln(5) \approx -0.61, \end{align*} $|f'(\ln(5))| \lt 1$, and the the equilibrium $x_n = \ln(5)$ is stable.

2. The below graph shows cobwebbing confirming these results.
3. As one can see from the cobwebbing, for any positive initial fish population $x_0$, the population $x_n$ will approach the stable equilibrium $\ln(5)$ as $n$ gets large.

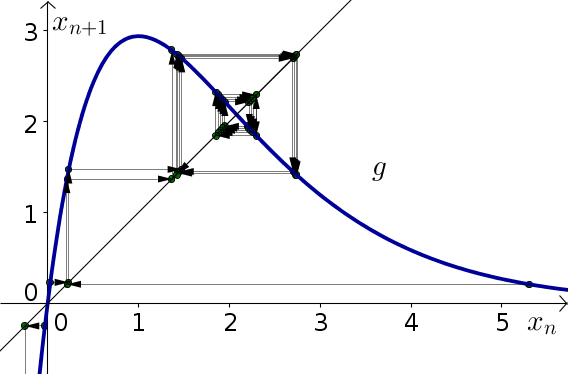
Problem 2

1. The dynamical system is already in the form $x_{n+1}=g(x_n)$ where $g(x)=5xe^{-x}$. The derivative is \begin{align*} g'(x) &= 8e^{-x} -8xe^{-x}\\ &= 8(1-x)e^{-x}. \end{align*} Since $g'(0)=8e^0 = 8 > 1$, the equilibrium $x_n=0$ is unstable. Since \begin{align*} g'(\ln(8)) &= 8(1-\ln(8))e^{-\ln(8)}\\ &= 8(1-\ln(8))e^{\ln(1/8)}\\ &= 8(1-\ln(8))/8\\ &= 1-\ln(8) \approx -1.08, \end{align*} $|g'(\ln(8))| \gt 1$, and the the equilibrium $x_n = \ln(8)$ is unstable.

2. The below graph shows cobwebbing confirming these results.
3. Due to the fact that $g'(\ln(8)) < -1$, the solution will oscillate as it moves away from the equilibrium. One can also see this from the cobwebbing. Since $g'(\ln(8))$ is so close to $-1$, the solution moves away from the equilibrium slowly, and it's hard to tell what is going on with the cobwebbing.

Problem 3

To calulate equilibria, let $s_{t+1}=s_t = E$, in which case $E$ must satisfy \begin{align*} E - E &= 0.5 E\left(1 - \frac{E}{300}\right)\\ 0 &= 0.5 E\left(1 - \frac{E}{300}\right)\\ E &=0 \quad \text{or} \quad \left(1 - \frac{E}{300}\right)= 0 \\ E &=0 \quad \text{or} \quad E = 300 \end{align*}

To calculate stability of these equilibria, we need to rewrite the dynamical system by solving for $s_{t+1}$ in terms of $s_t$. Adding $s_t$ to both sides, we obtain \begin{align*} s_{t+1} &= s_{t}+ 0.5 s_t\left(1 - \frac{s_t}{300}\right)\\ &= f(s_t) \end{align*} where $f(s) = s+0.5s(1-s/300)$. Since $f(s)$ is the updating function, we just need to calculate its derivative at the equilibria and see if it is between $-1$ and $1$. \begin{align*} f'(s) &= 1 + 0.5\left(1 - \frac{s}{300}\right) + 0.5s\left(-\frac{1}{300}\right)\\ &= 1.5 - \frac{s}{300} \end{align*}

For the equilibrium $s_t=0$, we need to check $f'(0)=1.5$. Since $f'(0) > 1$, the equilibrum $s_t=0$ is unstable.

For the equilibrium $s_t=300$, we calculate $f'(300) = 1.5 - 300/300 = 0.5$. Since $-1 < f'(300) < 1$, the equilibrium $s_t=300$ is stable.

If we started with an inital population of $s_0=400$ and waited a long time, the population will have decreased down to nearly 300.

Problem 4

1. To calulate equilibria, let $s_{t+1}=s_t = E$, in which case $E$ must satisfy \begin{align*} E - E &= r E\left(1 - \frac{E}{N}\right)\\ 0 &= r E\left(1 - \frac{E}{N}\right)\\ E &=0 \quad \text{or} \quad \left(1 - \frac{E}{N}\right)= 0 \\ E &=0 \quad \text{or} \quad E = N \end{align*}

2. To calculate stability of these equilibria, we need to rewrite the dynamical system by solving for $s_{t+1}$ in terms of $s_t$. Adding $s_t$ to both sides, we obtain \begin{align*} s_{t+1} &= s_{t}+ r s_t\left(1 - \frac{s_t}{N}\right)\\ &= f(s_t) \end{align*} where $f(s) = s+rs(1-s/N)$. Since $f(s)$ is the updating function, we just need to calculate its derivative at the equilibria and see if it is between $-1$ and $1$. \begin{align*} f'(s) &= 1 + r\left(1 - \frac{s}{N}\right) + rs\left(-\frac{1}{N}\right)\\ &= 1 + r - 2r\frac{s}{N} \end{align*}

   Let $r=1.5$ so that $f'(s) = 2.5 -3\frac{s}{N}$. For the equilibrium $s_t=0$, we need to check $f'(0)=2.5$. Since $f'(0) > 1$, the equilibrum $s_t=0$ is unstable.

   For the equilibrium $s_t=N$, we calculate $f'(N) = 2.5 - 3N/N = 2.5-3=-0.5$. Since $-1 < f'(N) < 1$, the equilibrium $s_t=N is stable.

3. Let $r=1.5$ and $N=500$. If we started with an inital population of $s_0=400$ and waited a long time, the population will have increased to nearly 500.

4. Now, let $r=3$ and keep $N$ a parameter so that $f'(s) = 4 -6\frac{s}{N}$. For the equilibrium $s_t=0$, we need to check $f'(0)=4$. Since $f'(0) > 1$, the equilibrum $s_t=0$ is unstable.

   For the equilibrium $s_t=N$, we calculate $f'(N) = 4 - 6N/N = 4-6=-2$. Since $f'(N) < -1$, the equilibrium $s_t=N$ is unstable.

5. For general $r$, remember from above that the derivative is $f'(s) = 1 + r - 2r\frac{s}{N}$. The derivative at the nonzero equilibrium $s_t=N$ is $f'(N) = 1+r-2rN/N = 1-r$. For this equilibrium to be stable we need that $-1 < 1-r < 1$ or $0 < r < 2$.

Problem 5

1. To calculate the equilibria, set $d_{t+1}=d_t = E$ and solve for $E$. \begin{align*} E &= 1.2 E - cE^2\\ 0 &= 0.2E -cE^2\\ 0 &= E(0.2-cE)\\ E &=0 \quad \text{or} \quad 0.2-cE = 0\\ E &=0 \quad \text{or} \quad E = 0.2/c \end{align*}
2. The dynamical system is already in the form $d_{t+1}=f(d_t)$ with $f(d) = 1.2d-cd^2$. We need to calculate its derivative at the equilibria: $f'(d) = 1.2 - 2cd$, $f'(0) = 1.2$, $f'(0.2/c) = 1.2-2c(0.2/c) = 1.2-2(0.2) = 0.8$. Since $f'(0) > 1$, the equilibrim $d_t=0$ is unstable. Since $|f'(0.2/c)|<1$, the equilibrium $d_t=0.2/c$ is stable.
3. The stability of the equilibria does not depend on the parameter $c$.
4. The stable equilibrium is $d_t=0.2/c$. To make this $200$, we need $0.2/c=200$ or $c = 0.2/200 = 0.001$.

Problem 6

1. To calculate the equilibria, set $l_{t+1}=l_t = E$ and solve for $E$. \begin{align*} E &= 4 E - cE^2\\ 0 &= 3E -cE^2\\ 0 &= E(3-cE)\\ E &=0 \quad \text{or} \quad 3-cE = 0\\ E &=0 \quad \text{or} \quad E = 3/c \end{align*}
2. The dynamical system is already in the form $l_{t+1}=f(l_t)$ with $f(l) = 4d-cl^2$. We need to calculate its derivative at the equilibria: $f'(l) = 4 - 2cl$, $f'(0) = 4$, $f'(3/c) = 4-2c(3/c) = 4-2(3) = -2$. Since $f'(0) > 1$, the equilibrim $l_t=0$ is unstable. Since $f'(3/c) < -1$, the equilibrium $l_t=3/c$ is also unstable.
3. The stability of the equilibria does not depend on the parameter $c$.
4. There are no stable equilibria, so the strategy will not succeed in bringing the number of locusts to a stable small population