Math Insight

Elementary discrete dynamical systems problems

 

Problem 1

Consider the dynamical system \begin{align*} x_{n+1} &= f(x_n) \quad \text{for $n=0,1,2,3, \ldots$ ,} \end{align*} where the function $f$ is graphed along with the diagonal $x_n = x_{n+1}$, below.

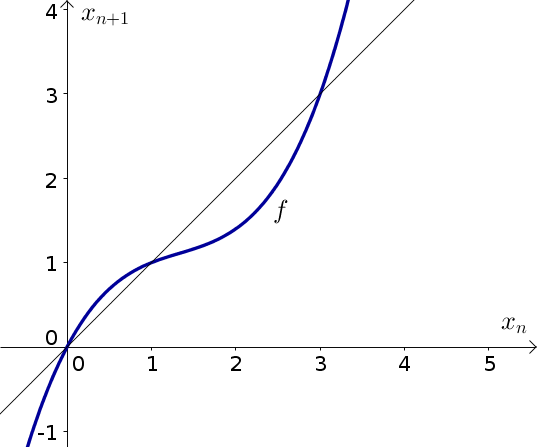
Discrete dynamical system example function 1
  1. Find the equilibria of the dynamical system. Indicate them on the graph along as well as list them with their approximate numerical values.
  2. Using cobwebbing, determine the stability of each equilibrium. Be sure to indicate the direction of your cobwebbing with arrows.

Problem 2

Consider the dynamical system \begin{align*} y_{t+1} &= g(y_t) \quad \text{for $t=0,1,2,3, \ldots$ ,} \end{align*} where the function $g$ is graphed along with the diagonal $y_t = y_{t+1}$, below.

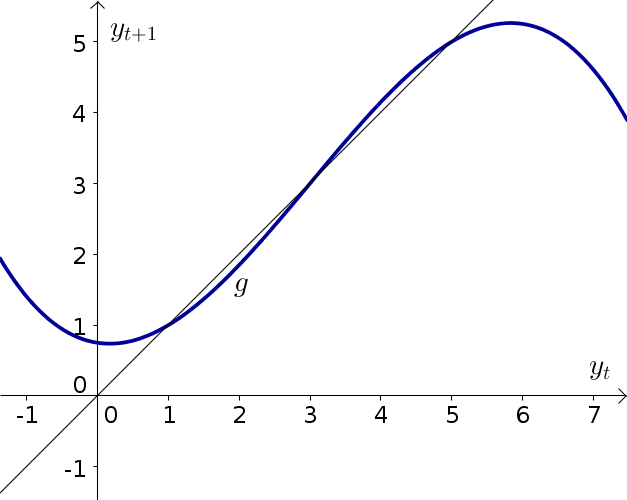
Discrete dynamical system example function 2
  1. Find the equilibria of the dynamical system. Indicate them on the graph along as well as list them with their approximate numerical values.
  2. Using cobwebbing, determine the stability of each equilibrium. Be sure to indicate the direction of your cobwebbing with arrows.

Problem 3

Consider the dynamical system \begin{align*} q_{t+1} - q_t = \frac{a q_t +b}{c}, \quad \text{for $t=0,1,2,3, \ldots$} \end{align*} where $a$, $b$, and $c$ are parameters. Find all equilibria.

Problem 4

Consider the dynamical system \begin{align*} m_{n+1} - m_n = \frac{b m_n +c}{d}, \quad \text{for $n=0,1,2,3, \ldots$} \end{align*} where $b$, $c$, and $d$ are parameters. Find all equilibria.

Problem 5

Consider the dynamical system \begin{align*} r_{t+1} = \frac{a r_t +b}{c}, \quad \text{for $t=0,1,2,3, \ldots$ } \end{align*} where $a$, $b$, and $c$ are parameters. Find all equilibria.

Problem 6

Consider the dynamical system \begin{align*} c_{t+1}-c_{t} = \frac{(c_t -a)(c_t-b)}{d}, \quad \text{for $t=0,1,2,3, \ldots$ } \end{align*} where $a$, $b$, and $d$ are parameters. Find all equilibria.

Problem 7

Consider the dynamical system \begin{align*} b_{n+1}-b_{n} = \frac{(b_n -\alpha)(b_n-\beta)(b_n-\gamma)}{\delta}, \quad \text{for $n=0,1,2,3, \ldots$ } \end{align*} where $\alpha$, $\beta$,$\gamma$, and $\delta$ are parameters. Find all equilibria.

Problem 8

Consider the dynamical system \begin{align*} m_{t+1} - m_t = -\frac{a}{b} m_t + \frac{a}{b}c, \quad \text{for $t=0,1,2,3, \ldots$ } \end{align*} where $a$, $b$, and $c$ are parameters.

  1. If one doubles the parameter $a$ and doubles the parameter $b$, how does the dynamical system change?
  2. If you know that value of $\lambda = \frac{a}{b}$, do you need to know the values of $a$ and $b$ individually to determine the evolution of the dynamical system? Why or why not?
  3. Rewrite the dynamical system in terms of $\lambda$ and $c$ (with no dependence on $a$ or $b$ individually).

Problem 9

Consider the dynamical system \begin{align*} l_{n+1} = \frac{ab}{c} l_n e^{-l_n a b /c}, \quad \text{for $n=0,1,2,3, \ldots$ } \end{align*} where $a$, $b$, and $c$ are parameters.

  1. If one doubles the parameter $a$ and doubles the parameter $c$, how does the dynamical system change?
  2. If one doubles the parameter $b$ and doubles the parameter $c$, how does the dynamical system change?
  3. If one doubles the parameter $a$ and halves the parameter $b$, how does the dynamical system change?
  4. If you know that value of $\gamma = \frac{ab}{c}$, do you need to know the values of $a$, $b$, and $c$ individually to determine the evolution of the dynamical system? Why or why not?
  5. Rewrite the dynamical system in terms of $\gamma$ (with no dependence on $a$, $b$, or $c$ individually).

Problem 10

What is an equilibrium of a dynamical system? What does it mean for an equilibrium to be stable? To be unstable?

Problem 11

Consider the dynamical system \begin{align*} h_{t+1} -h_t &= \frac{h_t(h_t -1)}{2} \quad \text{for $t=0,1,2,3, \ldots$ .} \end{align*}

  1. Find the equilibria.
    1. If $h_0 = -0.1$, calculate $h_1$, $h_2$, $h_3$, and $h_4$.
    2. If $h_0= 0.1$, calculate $h_1$, $h_2$, $h_3$, and $h_4$.
    3. Based on the above calculations, what can you infer about the stability of one of the equilibria?
    1. If $h_0 = 0.99$, calculate $h_1$, $h_2$, $h_3$, and $h_4$.
    2. If $h_0= 1.01$, calculate $h_1$, $h_2$, $h_3$, and $h_4$.
    3. Based on the above calculations, what can you infer about the stability of one of the equilibria?

Problem 12

Consider the dynamical system \begin{align*} S_{t+1} -S_t &= \frac{S_t(1-S_t)}{2} \quad \text{for $t=0,1,2,3, \ldots$ .} \end{align*}

  1. Find the equilibria.
    1. If $S_0 = -0.01$, calculate $S_1$, $S_2$, $S_3$, and $S_4$.
    2. If $S_0= 0.01$, calculate $S_1$, $S_2$, $S_3$, and $S_4$.
    3. Based on the above calculations, what can you infer about the stability of one of the equilibria?
    1. If $S_0 = 0.9$, calculate $S_1$, $S_2$, $S_3$, and $S_4$.
    2. If $S_0= 1.1$, calculate $S_1$, $S_2$, $S_3$, and $S_4$.
    3. Based on the above calculations, what can you infer about the stability of one of the equilibria?

Problem 13

Consider the dynamical system \begin{align*} q_{n+1} -q_n &= a q_n \quad \text{for $n=0,1,2,3, \ldots$ } \end{align*}

where $a$ is a parameter.

  1. Solve the dynamical system to give a formula for $q_n$ in terms of the initial condition $q_0$, the parameter $a$, and the number $n$.
  2. Find the equilibria.
  3. For each equilibrium, determine for which values of $a$ the equilibrium is stable.

Problem 14

Consider the dynamical system \begin{align*} p_{n+1} &= b p_n \quad \text{for $n=0,1,2,3, \ldots$ } \end{align*}

where $b$ is a parameter.

  1. Solve the dynamical system to give a formula for $p_n$ in terms of the initial condition $p_0$, the parameter $b$, and the number $n$.
  2. Find the equilibria.
  3. For each equilibrium, determine for which values of $b$ the equilibrium is stable.

One you have worked on a few problems, you can compare your solutions to the ones we came up with.

Thread navigation

Elementary dynamical systems

Similar pages

See also