Image: Two curves over a conservative field
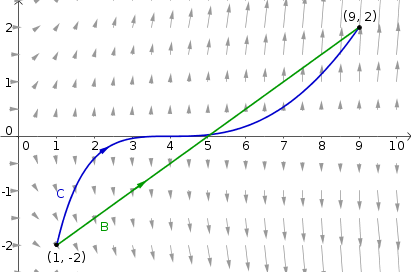
The line integral of a conservative field over two curves between the same pair of points will be identical.
The curve $\dlc$ (in blue) is parametrized by $\dllp(t) = (t^2,2(t-2)^3)$ for $1 \le t \le 3$. The curve $\adlc$ (in green) is parametrized by $\adllp(t)=(1+8t,4t-2)$ for $0 \le t \le 1$. Both curves start at $(1,-2)$ and end at $(9,2)$, so the line integral of a conservative vector field will be the same over both curves. The pictured vector field is $\dlvf(x,y) = (y^2,2xy)$ which is the gradient of $f(x,y)=xy^2$ and so conservative. The line integral over both $\dlc$ and $\adlc$ is $f(9,2)-f(1,-2) = 32.$
Image file: gradient_theorem_example_curves.png
Source image file: gradient_theorem_example_curves.ggb
Source image type: Geogebra
Image links
This image is found in the pages