The influence of network structure on correlations
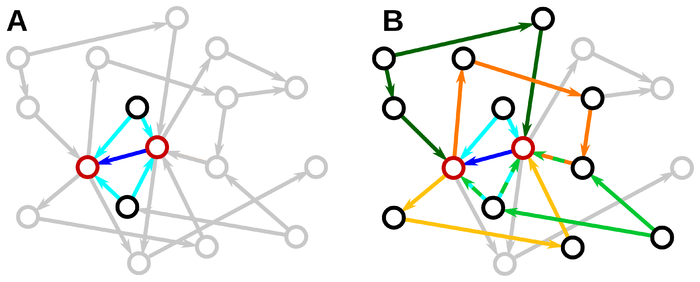
Pernice et al. have developed an approach to analyze the influence of different network motifs on correlations between the activity of a pair of nodes.1
To get the flavor of their approach, let's imagine a very simplified model, where the $N$-dimensional $\vc{x}$ is the activity of the $N$ network nodes. Image that, if the network were uncoupled the activity of the nodes would be $\vc{x}_0$. With the coupling, the activity $\vc{x}$ satisfies this simple linear self-consistency equation $$\vc{x} = \vc{x}_0 + wA\vc{x},$$ where $A$ is the adjacency matrix and the scalar $w$ is the weighting of the effect of each connection.
We can easily solve this equation for $\vc{x}$ in terms of the uncoupled activity $\vc{x}_0$. $$\vc{x} = (I-wA)^{-1}\vc{x}_0$$
For simplicity, assume that the $\vc{x}$ are all mean zero. We can calculate their correlation as $E(\vc{x}\vc{x}^T)$, where $E(\cdot)$ is the expected value from measuring the activity over many experiments.
The correlation satisfies $$E(\vc{x}\vc{x}^T) = (I-wA)^{-1}E(\vc{x}_0\vc{x}_0^T)(I-wA^T)^{-1}$$ which we can rewrite as $$C= (I-wA)^{-1}C_0(I-wA^T)^{-1}$$
$C_0$ the correlation if there were no coupling. Since the nodes would be independent in this case, it is a diagonal matrix. Let's assume that the network is statistically homogeneous so that all diagonal entries of $C_0$ are the same, equal to the constant $c_0$: $C_0 = c_0 I$. Then we can rewrite our equation as $$\frac{C}{c_0}= (I-wA)^{-1}(I-wA^T)^{-1}.$$
If we assume weak coupling so that $wA$ is small, then we can expand in a power series. $$\frac{C}{c_0} = \sum_{i,j=0}^\infty w^{i+j} A^i(A^T)^i.$$
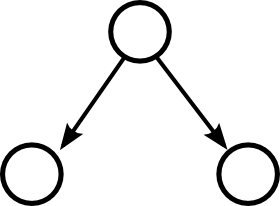
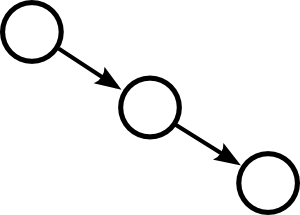
Each term $A^i(A^T)^i$ represents different network motifs. For example $AA^T$ represents divergence motif, and $A^2$ or $(A^T)^2$ represent chains of two edges. In this way, you can examine how different motifs influence the correlations.
For example, if you consider just motifs of two edges, then you find that just the divergent motif and the chain motif influence correlations.