Solutions to single autonomous differential equation problems
Problem 1
- A sketch of the vector field on the phase line, showing in which intervals $x(t)$ is increasing or decreasing.

- The equilibria are the points where $f(x)=0$. They are $x^*=1$, $x^*=2$, $x^*=3$, and $x^*=4$, and are shown by the pink circles on the above phase line. Since the vector field is pointing towards $x^*=1$ and $x^*=3$, these equilibria are stable. Since the vector field is pointing away from $x^*=2$ and $x^*=4$, these equilibria are unstable.
-
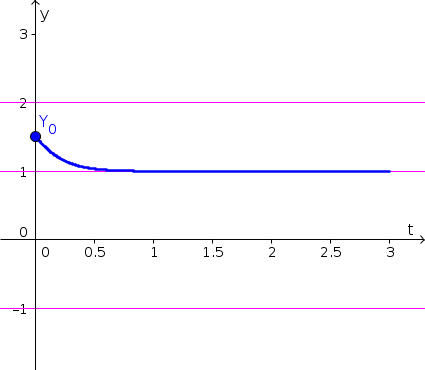
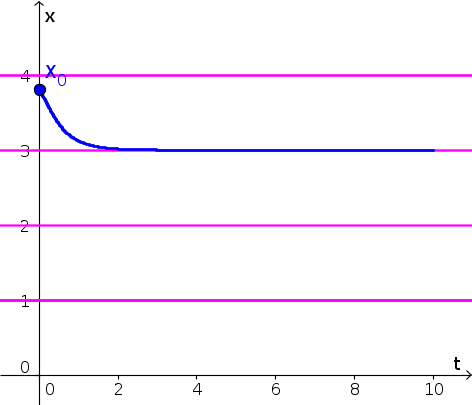
- Since $x(t)$ is decreasing in the interval $3 \lt x \lt 4$, the solution with initial condition $x(0)=3.8$ decreases, getting closer and closer to the equilibria $x^*=3$, as shown by the blue curve, below. Equilibria are shown as pink horizontal lines.
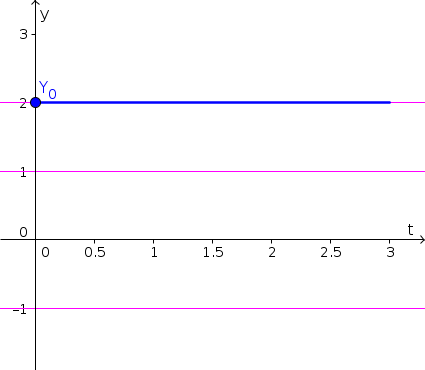
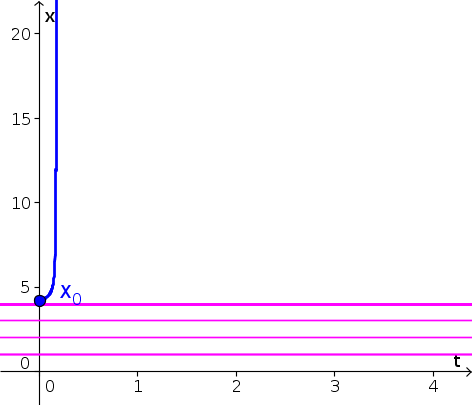
- Since $x(t)$ is increasing for $x \gt 4$, the solution with initial condition $x(0)=4.2$ increases, as shown by the blue curve, below. (We extrapolated that $f(x)$ increases even further for $x \gt 5$, though, strictly speaking, the graph didn't give information for $x \gt 5$. Your really just need to show that $x(t)$ increases past 5.) Equilibria are shown as pink horizontal lines.
- Since $x(t)$ is decreasing in the interval $3 \lt x \lt 4$, the solution with initial condition $x(0)=3.8$ decreases, getting closer and closer to the equilibria $x^*=3$, as shown by the blue curve, below. Equilibria are shown as pink horizontal lines.
Problem 2
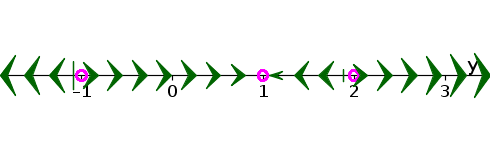
- A sketch of the vector field on the phase line, showing in which intervals $z(t)$ is increasing or decreasing.

- The equilibria are $z^*=1$ and $z^*=4$, and are shown by the pink circles on the above phase line. Since the vector field is pointing toward $z^*=1$, this equilibrium is stable. Since the vector field is pointing away from $z^*=4$, this equilibrium is unstable.
-
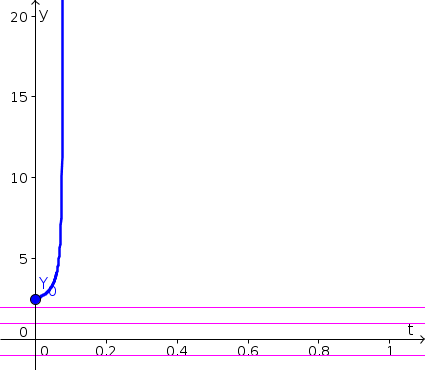
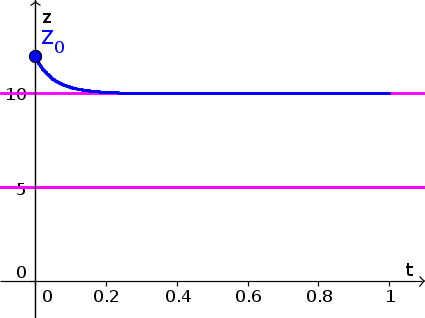
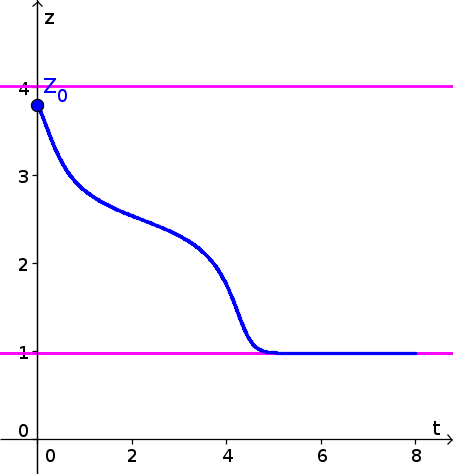
- Since $z(t)$ is decreasing in the interval $1 \lt z \lt 4$, the solution with $z(0)=3.8$ decreases. Initially, it decreases at a fast rate, but its speed decreases, reaching its slowest speed when $z(t)=2.5$. As $z(t)$ decreases past 2.5, the picks up speed for a little bit until it gets close to the equilibrium $z^*=1$. It approaches this equilibrium as $t$ increases. The resulting form of $z(t)$ is shown by the blue curve, below. Equilibria are shown as pink horizontal lines.
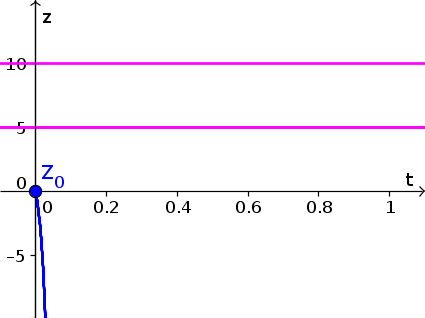
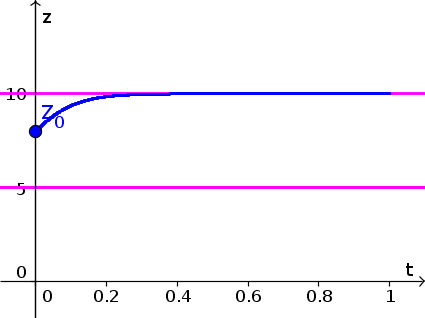
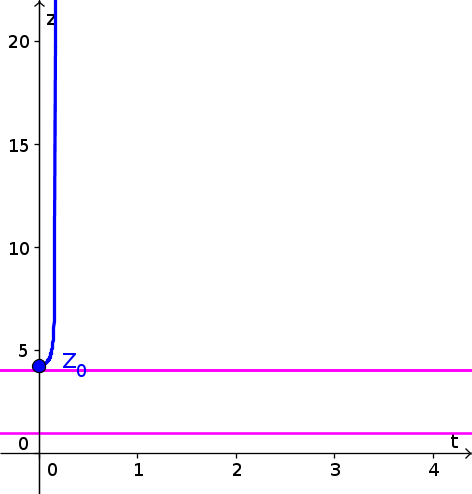
- Since $z(t)$ is increasing for $z \gt 4$, the solution with initial condition $z(0)=4.2$ increases, as shown by the blue curve, below. (We extrapolated that $h(z)$ increases even further for $z \gt 5$, though, strictly speaking, the graph didn't give information for $z \gt 5$. Your really just need to show that $z(t)$ increases past 5.) Equilibria are shown as pink horizontal lines.
- Since $z(t)$ is decreasing in the interval $1 \lt z \lt 4$, the solution with $z(0)=3.8$ decreases. Initially, it decreases at a fast rate, but its speed decreases, reaching its slowest speed when $z(t)=2.5$. As $z(t)$ decreases past 2.5, the picks up speed for a little bit until it gets close to the equilibrium $z^*=1$. It approaches this equilibrium as $t$ increases. The resulting form of $z(t)$ is shown by the blue curve, below. Equilibria are shown as pink horizontal lines.
Problem 3
Consider the dynamical system \begin{align*} \diff{y}{t} = 3(y-2)(y-1)(y+1). \end{align*}
- The equilibria $y^*=-1$, $y^*=1$, and $y^*=2$. To use the stability theorem, we need to calculate the derivative of the right hand side of the equation. Let $f(y) = 3(y-2)(y-1)(y+1)$. Then, \begin{align*} f'(y) &=\diff{}{y}[3(y-2)(y-1)(y+1)]\\ &= 3\left(\diff{}{y}(y-2)\right)(y-1)(y+1) + 3(y-2)\left(\diff{}{y}[(y-1)(y+1)]\right)\\ &= 3(y-1)(y+1) + 3(y-2)\Biggl(\left[\diff{}{y}(y-1)\right](y+1)\\ &\qquad+ (y-1)\left[\diff{}{y}(y+1)\right]\Biggr)\\ &= 3(y-1)(y+1) + 3(y-2)(y+1) + 3(y-2)(y-1) \end{align*} Since $f'(-1) = 0 +0 +3(-1-2)(-1-1) = 18 \gt 0$, the equilibrium $y^*=-1$ is unstable. Since $f'(1) = 0 + 3(1-2)(1+1)+0 = -6 \lt 0$, the equilibrium $y^*=1$ is stable. Since $f'(2) = 3(2-1)(2+1)+0+0= 9 \gt 0$, the equilibrium $y^*=2$ is unstable.
- A sketch of the vector field on the phase line, showing in which intervals $y(t)$ is increasing or decreasing
Problem 4
Consider the differential equation \begin{align*} \diff{z}{t} = -3(z-5)(z-10). \end{align*}
- The equilibria are $z^*=5$ and $z^*=10$. To calculate their stability, we differentiate the right hand side, $g(z)=-3(z-5)(z-10)$: \begin{align*} g'(z) &= -3 \diff{(z-5)}{z}(z-10) -3(z-5)\diff{(z-10)}{z}\\ &= -3(z-10)-3(z-5). \end{align*} Since $g'(5)=-3(5-10)=15 \gt 0$, the equilibrium $z^*=5$ is unstable. Since $g'(10)=-3(10-5) = -15 \lt 0$, the equilibrium $z^*=10$ is stable.
- A sketch of the vector field on the phase line.

Problem 5
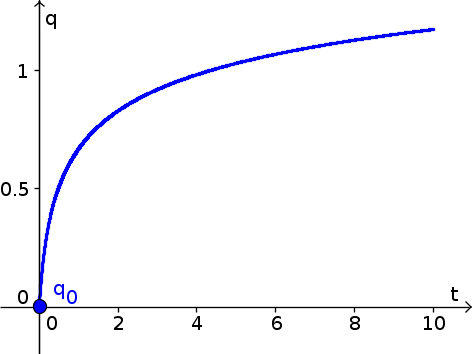
The equilibria are points where $e^{-q^2-3q+1}=0$. Since the exponential function is always positive, there are no equilibria. A graph of the solution $q(t)$ with initial condition $q(0)=0$ is shown below. Since $e^{-q^2-3q+1}$ gets very small as $q$ increases, the function $q(t)$ slows down.
Problem 6
The equilibria $r^*$ must satisfy $-r^* e^{r^*}=0$. Since $e^{r^*}$ is never zero, the only equilibrium is $r^*=0$.
Since $\diff{}{r}(-re^r) = (-1-r)e^r$ and this expression is $-1 \lt 0$ when $r=0$, the equilibrium $r^*=0$ is stable.
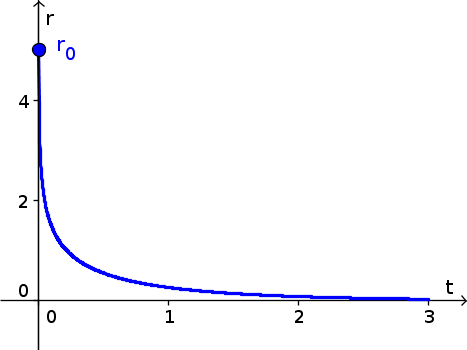
The graph of the solution $r(t)$ with initial condition $r(0)=5$ is shown below.
Problem 7
Denote the right hand side of the differential equation by $f(m)=e^{-m^2}$. Then, the Forward Euler algorithm gives $m(t+\Delta t)$ in terms of the solution $m(t)$ at the earlier time $t$ and the slope $f(m(t))$: \begin{align*} m(t+\Delta t) \approx m(t) + f(m(t))\Delta t. \end{align*} Given that $m(0)=-1$, $f(m(0)) = f(-1)=e^{-1}$, and $\Delta t=1$, the first Euler step gives \begin{align*} m(1) \approx -1 + e^{-1}\cdot 1 \approx -0.6321. \end{align*}
Next, since $f(-0.6321)=e^{-(-0.6321)^2} \approx 0.6706$, the second Euler step gives \begin{align*} m(2) \approx -0.6321 + 0.6706\cdot 1 \approx 0.0385. \end{align*}
Lastly, since $f(0.0385) =e^{-0.0385^2} \approx 0.9985$, the third Euler step gives \begin{align*} m(3) \approx 0.0385 + 0.9985 \cdot 1 \approx 1.037. \end{align*}
Problem 8
Let $g(w)=1-e^{-w}$. The Forward Euler algorithm is \begin{align*} w(t+\Delta t) \approx w(t) + g(w(t))\Delta t. \end{align*}
Starting with $w(0)=-1$, we calculate that $g(-1) \approx -1.7183$ and \begin{align*} w(0.5) \approx -1 -1.7183 \cdot 0.5 \approx -1.8591. \end{align*} Since $g(-1.8591) \approx -5.4182$, the second step is \begin{align*} w(1) \approx -1.8591 - -5.4182 \cdot 0.5 \approx -4.5683. \end{align*} Since $g(-4.5683) \approx -95.3754$, the third step is \begin{align*} w(1.5) \approx -4.5683 -95.3754 \cdot 0.5 \approx -52.256. \end{align*} Since $$g(-52.256) \approx -49485289552291400000000 \approx -4.9485 \times 10^{22},$$ the fourth step is \begin{align*} w(2) \approx -52.256 - 4.9485 \times 10^{22} \times 0.5 \approx -2.4743 \times 10^{22}. \end{align*} The function is plummeting to hugely negative numbers very fast. (Maybe we should have stopped at $w(1.5)$!)
Problem 9
- The equilibria are $u=0$ and $u=2$. Differentiating $h(u)=u(2-u)$, we calculate that $h'(u)=2-2u$. Since $h'(0)=2 \gt 0$, the equilbrium $u=0$ is unstable. Since $h'(2)=-2 \lt 0$, the equilibrium $u=2$ is stable.
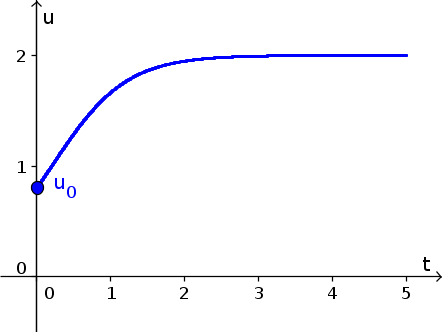
- The solution $u(t)$ with initial condition $u(0)=0.8$ is graphed below.
- When $\Delta t = 2$, the Forward Euler time step is $u(t+2) = u(t) + 2h(u(t))$. Since $h(u(0))=h(0.8)=0.96$, the first step is $$u(2) \approx 0.8 + 2 \cdot 0.96 = 2.72.$$ Since $h(2.72)=-1.9584$, the second step is $$u(4) \approx 2.72 + 2(-1.9584) = -1.1968.$$ Since $h(-1.196) \approx -3.8260$, the third step is $$u(6) \approx -1.1968 +2 (-3.8260) \approx -8.8487.$$ Since $h(-8.8487) \approx -95.9961$, the fourth step is $$u(8) \approx -8.8487 + 2(-95.9961) \approx -200.8509.$$ This behavior does not match the previous result. The Forward Euler solution is decreasing rapidly instead of converging to the stable equilibrium $u^*=2$.
- When $\Delta t = 1$, the Forward Euler time step is $u(t+1) = u(t) + h(u(t))$. Since, as before, $h(u(0))=h(0.8)=0.96$, the first step is $$u(1)\approx0.8+ 0.96 = 1.76.$$ Since $h(1.76)=0.4224$, the second step is $$u(2) \approx 1.76 + 0.4224 = 2.1824.$$ Since $h(2.1824) \approx -0.3981$, the third step is $$u(3) \approx 2.1824 -0.3981 \approx 1.7843.$$ Since $h(1.7843) \approx 0.3848$, the fourth step is $$u(4) \approx 1.7843 + 0.3848 \approx 2.1592.$$ The solution does not match the behavior of the previous result. The Forward Euler solution seems to be oscillationg between 1.78 and 2.16 rather than converging steadily to the stable equilibrium $u^*=2$.
- When $\Delta t=0.5$, the Forward Euler time step is $u(t+0.5) = u(t) + 0.5h(u(t))$. Since, as before, $h(u(0))=h(0.8)=0.96$, the first step is $$u(1/2)\approx 0.8+ 0.5 \cdot 0.96 = 1.28.$$ Since $h(1.28) = 0.9216$, the second step is $$u(1) \approx 1.28 + 0.5 \cdot 0.9216 - 1.7408.$$ Since $h(1.7408) \approx 0.4512$, the third step is $$u(3/2) \approx 1.7408 + 0.5 \cdot 0.4512 \approx 1.9664.$$ Since $h(1.9664) \approx 0.0661$, the fourth step is $$u(2) \approx 1.9664 + 0.5 \cdot 0.0661 \approx 1.9994.$$ The Foward Euler suolution is matching the previous result. Both solutions are converging steadily to the equilibrium $u^*=2$.