Applet: Particle on helix with magnet and tangent vector
Applet loading
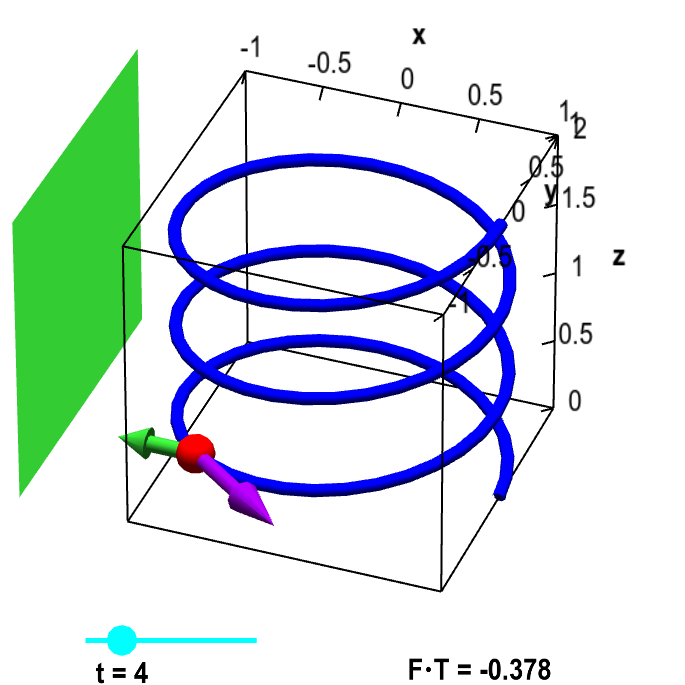
The blue helix is parametrized by $\dllp(t) = (\cos t, \sin t, t/(3\pi))$, for $0 \le t \le 6\pi$. For a given value of $t$ (changed by the cyan point on the slider), the red point represents a magnetic bead at point $\dllp(t)$. The purple vector represents the tangent vector $\vc{T}$ in the direction of the particle's movement for increasing $t$. The green rectangle represents a large magnet, which induces the constant magnetic field represented by the vector field $\dlvf(x,y,z) = (-1/2, 0, 0)$ and illustrated with the green vector. The work done by the magnetic field on the particle is determined by the component $\dlvf \cdot \vc{T}$ of the magnetic field vector $\dlvf$ in the direction of the tangent vector $\vc{T}$, the value of which is shown in the lower right corner.
Applet links
This applet is found in the pages
Notation systems
More information on notation systems
General information about three.js applets
The applet was made using three.js and requires Javascript as well as a browser that supports WebGL. For most three.js applets, you can drag with the mouse to rotate the view, drag with the right button to pan, and zoom in/out with the mouse wheel. Many applets contain points that you can drag to change values of variables.