Applet: Ice cream cone region with shadow
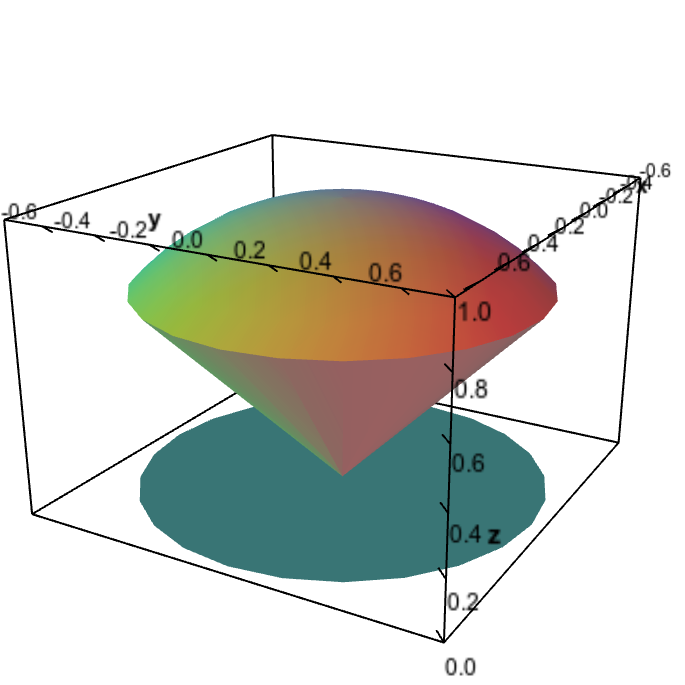
Applet loading
The ice cream cone region is bounded above by the half-sphere $z=\sqrt{1-x^2-y^2}$ and bounded below by the cone $z=\sqrt{x^2+y^2}$. The two surfaces intersect along a circle defined by $x^2+y^2=1/2$ and $z=1/\sqrt{2}$, which is the widest part of the ice cream cone. Therefore, the shadow of the ice cream cone region parallel to the $xy$-plane is the disk of radius $1/\sqrt{2}$ described by $x^2+y^2 \le 1/2$.
Applet links
This applet is found in the pages
General information about three.js applets
The applet was made using three.js and requires Javascript as well as a browser that supports WebGL. For most three.js applets, you can drag with the mouse to rotate the view, drag with the right button to pan, and zoom in/out with the mouse wheel. Many applets contain points that you can drag to change values of variables.