Applet: Non-differentiable function with partial derivatives and no tangent plane
Applet loading
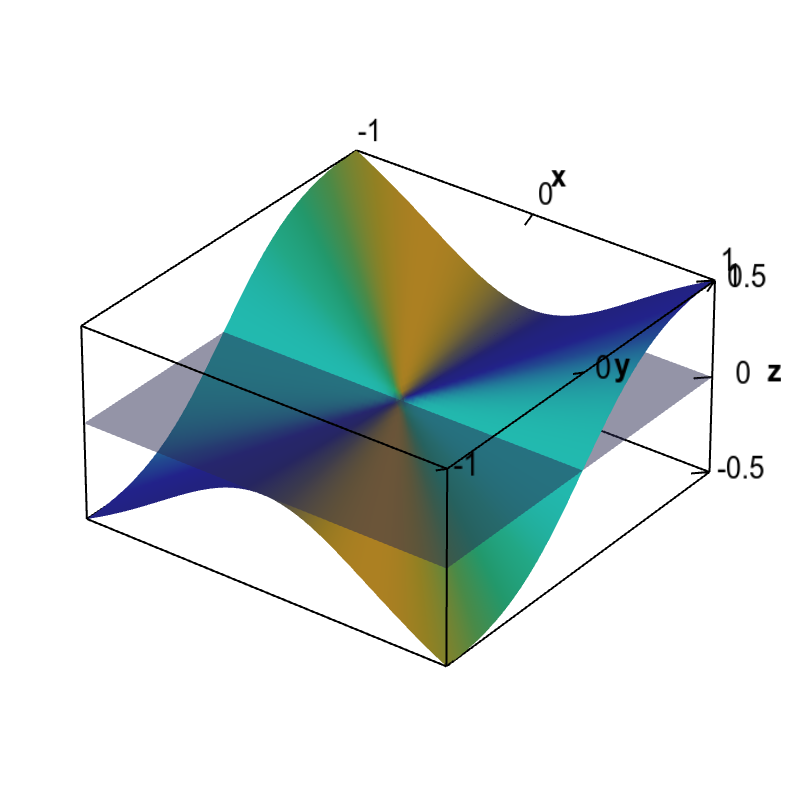
A function that is not differentiable at the origin is shown with the only possibility for a tangent plane at the origin. As the partial derivatives are zero at the origin, this candidate plane is a horizontal plane. However, this plane is not tangent since the slopes of this function coming to the origin along different directions are not zero.
The function is \begin{align*} f(x,y) = \begin{cases} \displaystyle \frac{x^2y}{x^2+y^2} & \text{if } (x,y) \ne (0,0)\\ 0 & \text{if } (x,y) = (0.0). \end{cases} \end{align*} We show that the above claim that the partial derivatives are zero at the origin is indeed true. Since this function is defined in a piecewise fashion around the origin, we have to use the limit definition of the partial derivatives, \begin{align*} \pdiff{f}{x}(0,0) &= \lim_{h \rightarrow 0} \frac{f(0+h,0)-f(0,0)}{h}\\ \pdiff{f}{y}(0,0) &= \lim_{h \rightarrow 0} \frac{f(0,0+h)-f(0,0)}{h}. \end{align*}
Since $f(0,0)=0$, $f(0+h,0)=f(h,0) = 0$, and $f(0,0+h)=f(0,h)=0$, we calculate that \begin{align*} \pdiff{f}{x}(0,0) &= \lim_{h \rightarrow 0} \frac{f(0+h,0)-f(0,0)}{h}\\ &= \lim_{h \rightarrow 0} \frac{0- 0}{h} = \lim_{h \rightarrow 0} 0 =0,\\ \pdiff{f}{y}(0,0) &= \lim_{h \rightarrow 0} \frac{f(0,0+h)-f(0,0)}{h}\\ &= \lim_{h \rightarrow 0} \frac{0- 0}{h} = \lim_{h \rightarrow 0} 0 =0. \end{align*}Applet links
This applet is found in the pages
General information about three.js applets
The applet was made using three.js and requires Javascript as well as a browser that supports WebGL. For most three.js applets, you can drag with the mouse to rotate the view, drag with the right button to pan, and zoom in/out with the mouse wheel. Many applets contain points that you can drag to change values of variables.