Applet: Slopes illustrating the discontinuous partial derivatives of a non-differentiable function
Applet loading
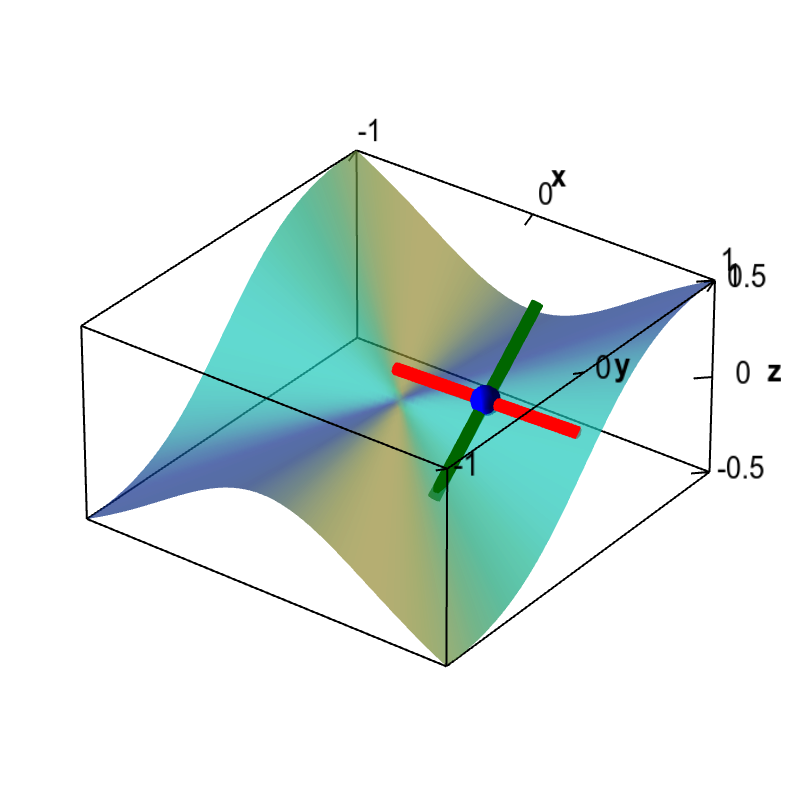
Although this function, shown as a surface plot, has partial derivatives defined everywhere, the partial derivatives are discontinuous at the origin. The colored line segments around the movable blue point illustrate the partial derivatives. The slope of the red line is $\pdiff{f}{x}$ while the slope of the dark green line is $\pdiff{f}{y}$. As you move the point near the origin using the mouse, the slopes will change sharply, reflecting the fact that they are discontinuous around the origin. Since the function is not differentiable at the origin, i.e., there is no tangent plane at the origin, we know from the differentiability theorem that the partial derivatives must not be continuous there.
This function is \begin{align*} f(x,y) = \begin{cases} \displaystyle \frac{x^2y}{x^2+y^2} & \text{if } (x,y) \ne (0,0)\\ 0 & \text{if } (x,y) = (0.0). \end{cases} \end{align*} Its partial derivatives are \begin{align*} \pdiff{f}{x}(x,y) &= \begin{cases} \displaystyle \frac{2 x y}{x^2+y^2}-\frac{2 x^3 y}{\left(x^2+y^2\right)^2} \ & \text{if } (x,y) \ne (0,0)\\ 0 & \text{if } (x,y) = (0.0). \end{cases} \\ \pdiff{f}{y}(x,y) &= \begin{cases} \displaystyle \frac{x^2}{x^2+y^2}-\frac{2 x^2 y^2}{\left(x^2+y^2\right)^2} \ & \text{if } (x,y) \ne (0,0)\\ 0 & \text{if } (x,y) = (0.0). \end{cases} \end{align*} (One must use the limit definition to calculate the partial derivatives at the origin.)
Applet links
This applet is found in the pages
General information about three.js applets
The applet was made using three.js and requires Javascript as well as a browser that supports WebGL. For most three.js applets, you can drag with the mouse to rotate the view, drag with the right button to pan, and zoom in/out with the mouse wheel. Many applets contain points that you can drag to change values of variables.