Applet: Scalar triple product
Applet loading
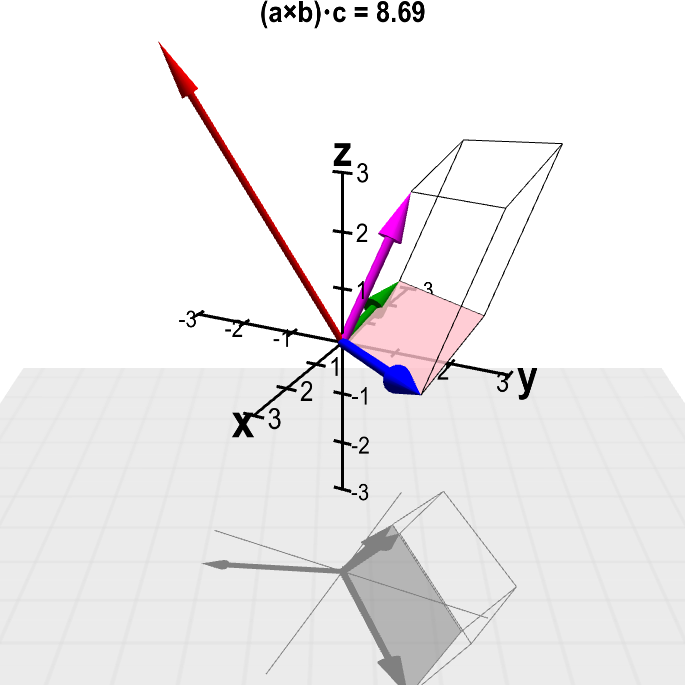
The value of the scalar triple product $(\color{blue}{\vc{a}} \times \color{green}{\vc{b}}) \cdot \color{magenta}{\vc{c}}$ is shown at the top, where the vectors $\color{blue}{\vc{a}}$ (in blue), $\color{green}{\vc{b}}$ (in green), and $\color{magenta}{\vc{c}}$ (in magenta) can changed by dragging their tips with the mouse. The volume of the spanned parallelepiped (outlined) is the magnitude $\|(\color{blue}{\vc{a}} \times \color{green}{\vc{b}}) \cdot \color{magenta}{\vc{c}}\|$. The cross product $\color{blue}{\vc{a}} \times \color{green}{\vc{b}}$ is shown by the red vector; its magnitude is the area of the highlighted parallelogram, which is one face of the parallelepiped.
The three-dimensional perspective of this graph is hard to perceive when the graph is still. If you keep the figure rotating by dragging it with the mouse, you'll see it much better. (Apologies to color blind people for reliance on colors.)
Applet links
This applet is found in the pages
General information about three.js applets
The applet was made using three.js and requires Javascript as well as a browser that supports WebGL. For most three.js applets, you can drag with the mouse to rotate the view, drag with the right button to pan, and zoom in/out with the mouse wheel. Many applets contain points that you can drag to change values of variables.