Simply connected definition
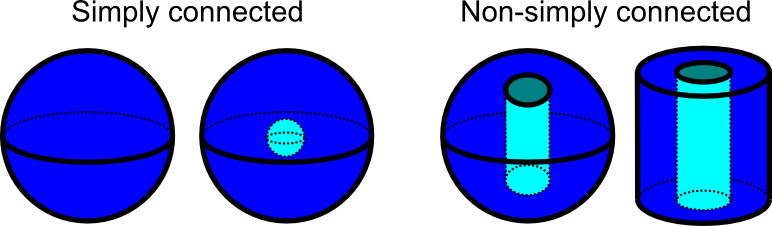
A simply connected domain is a path-connected domain where one can continuously shrink any simple closed curve into a point while remaining in the domain.
For two-dimensional regions, a simply connected domain is one without holes in it.
For three-dimensional domains, the concept of simply connected is more subtle. A simply connected domain is one without holes going all the way through it. However, a domain with just a hole in the middle (like a ball whose center is hollow) is still simply connected, as we can continuously shrink any closed curve to a point by going around the hole and remaining in the domain. On the other hand, a ball with a hole drilled all the way through it, or a spool with a hollow central axis, is not simply connected. A closed curve that went around the hole could not be shrunk to a point while remaining in the domain. There is no way for the curve to bypass the the hole so it remains stuck around it.
.