Applet: Cross product
Applet loading
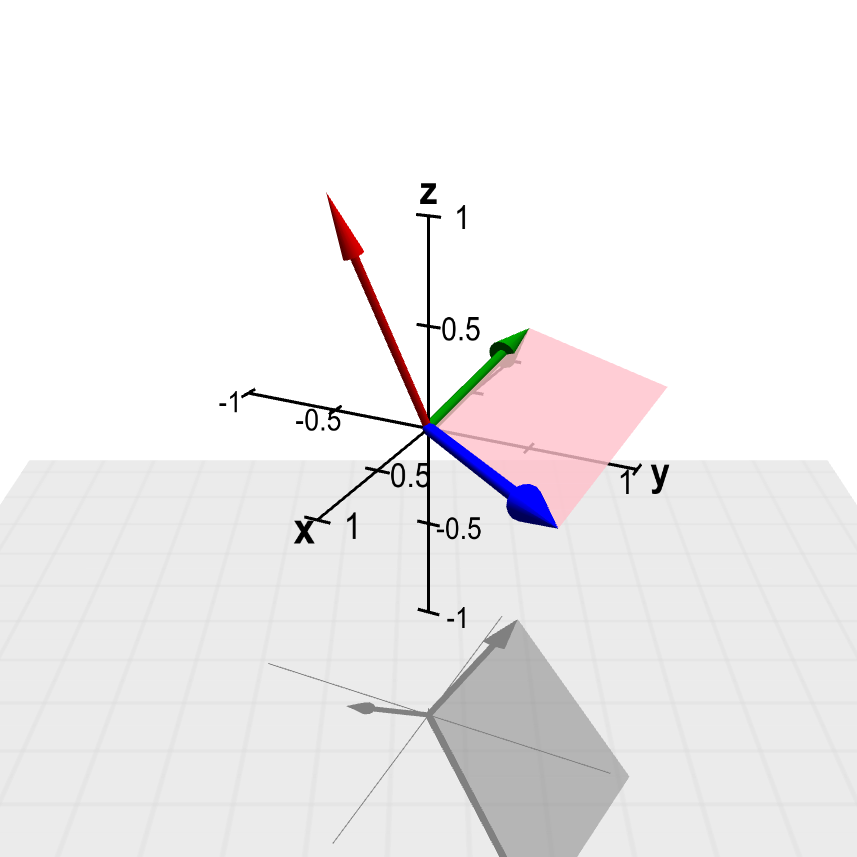
The vector $\color{red}{\vc{c}}$ (in red) is the cross product of the vectors $\color{blue}{\vc{a}}$ (in blue) and $\color{green}{\vc{b}}$ (in green), $\color{red}{\vc{c}} = \color{blue}{\vc{a}} \times \color{green}{\vc{b}}$. The parallelogram formed by $\color{blue}{\vc{a}}$ and $\color{green}{\vc{b}}$ is pink on the side where the cross product $\color{red}{\vc{c}}$ points and purple on the opposite side. Using the mouse, you can drag the arrow tips of the vectors $\color{blue}{\vc{a}}$ and $\color{green}{\vc{b}}$ to change these vectors. See how the cross product $\color{red}{\vc{c}}$ and the parallelogram change in response. (You cannot change the red cross product vector $\color{red}{\vc{c}}$ directly.) The three-dimensional perspective of this graph may be easier to perceive if you keep the figure rotating by dragging it with your mouse.
Notice that the area of the parallelogram (and hence the magnitude of the cross product) go to zero as $\vc{a}$ and $\vc{b}$ approach parallel (where the term “parallel” also includes what you might think as anti-parallel). You can also verify that the applet demonstrates $\vc{b} \times \vc{a} = - \vc{a} \times \vc{b}$ and $\vc{a} \times \vc{a} = \vc{0}$, which are important properties of the cross product.
Applet links
This applet is found in the pages
General information about three.js applets
The applet was made using three.js and requires Javascript as well as a browser that supports WebGL. For most three.js applets, you can drag with the mouse to rotate the view, drag with the right button to pan, and zoom in/out with the mouse wheel. Many applets contain points that you can drag to change values of variables.