The cross product
There are two ways to take the product of a pair of vectors. One of these methods of multiplication is the cross product, which is the subject of this page. The other multiplication is the dot product, which we discuss on another page.
The cross product is defined only for three-dimensional vectors. If $\vc{a}$ and $\vc{b}$ are two three-dimensional vectors, then their cross product, written as $\vc{a} \times \vc{b}$ and pronounced “a cross b,” is another three-dimensional vector. We define this cross product vector $\vc{a} \times \vc{b}$ by the following three requirements:
- $\vc{a} \times \vc{b}$ is a vector that is perpendicular to both $\vc{a}$ and $\vc{b}$.
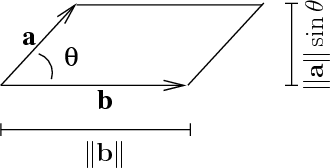
- The magnitude (or length) of the vector $\vc{a} \times \vc{b}$, written as $\|\vc{a} \times \vc{b}\|$, is the area of the parallelogram spanned by $\vc{a}$ and $\vc{b}$ (i.e. the parallelogram whose adjacent sides are the vectors $\vc{a}$ and $\vc{b}$, as shown in below figure).
- The direction of $\vc{a} \times \vc{b}$ is determined by the right-hand rule. (This means that if we curl the fingers of the right hand from $\vc{a}$ to $\vc{b}$, then the thumb points in the direction of $\vc{a} \times \vc{b}$.)
The below figure illustrates how, using trigonometry, we can calculate that the area of the parallelogram spanned by $\vc{a}$ and $\vc{b}$ is \begin{align*} \|\vc{a}\| ~ \|\vc{b}\| \sin\theta, \end{align*} where $\theta$ is the angle between $\vc{a}$ and $\vc{b}$. The figure shows the parallelogram as having a base of length $\|\vc{b}\|$ and perpendicular height $\|\vc{a}\| \sin \theta$.
This formula shows that the magnitude of the cross product is largest when $\vc{a}$ and $\vc{b}$ are perpendicular. On the other hand, if $\vc{a}$ and $\vc{b}$ are parallel or if either vector is the zero vector, then the cross product is the zero vector. (It is a good thing that we get the zero vector in these cases so that the above definition still makes sense. If the vectors are parallel or one vector is the zero vector, then there is not a unique line perpendicular to both $\vc{a}$ and $\vc{b}$. But since there is only one vector of zero length, the definition still uniquely determines the cross product.)
Below is an applet that helps illustrate how the cross product works. Although it is admittedly hard to manipulate in a precise manner, you can convince yourself that the above properties of the cross product are satisfied by the cross product vector shown in the applet.
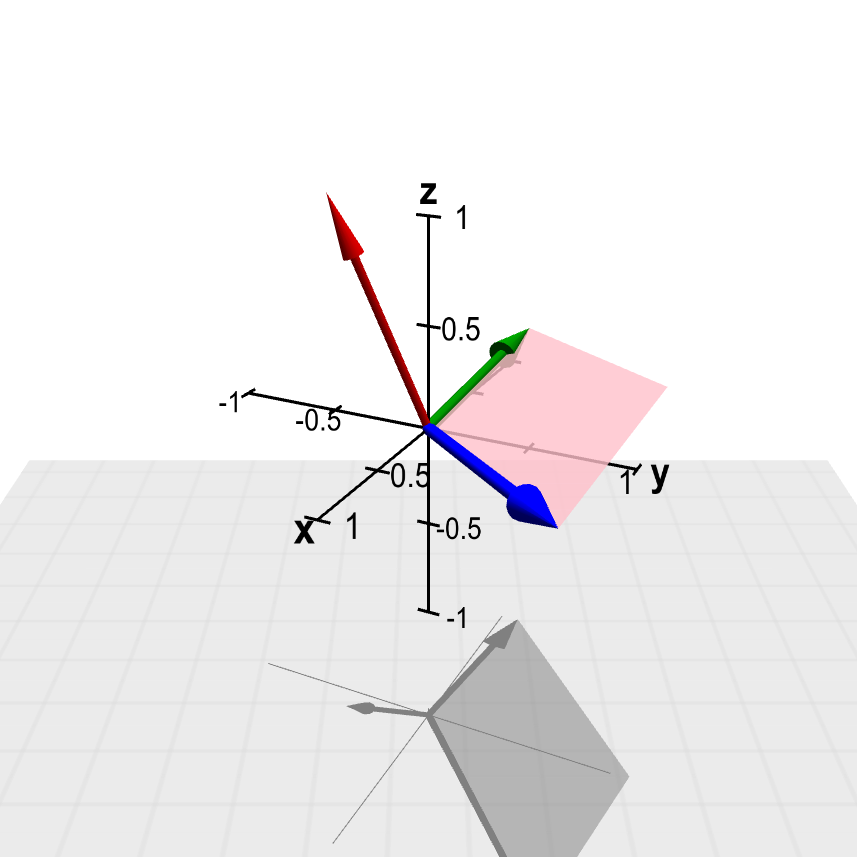
Applet loading
Cross product. The vector $\color{red}{\vc{c}}$ (in red) is the cross product of the vectors $\color{blue}{\vc{a}}$ (in blue) and $\color{green}{\vc{b}}$ (in green), $\color{red}{\vc{c}} = \color{blue}{\vc{a}} \times \color{green}{\vc{b}}$. The parallelogram formed by $\color{blue}{\vc{a}}$ and $\color{green}{\vc{b}}$ is pink on the side where the cross product $\color{red}{\vc{c}}$ points and purple on the opposite side. Using the mouse, you can drag the arrow tips of the vectors $\color{blue}{\vc{a}}$ and $\color{green}{\vc{b}}$ to change these vectors. See how the cross product $\color{red}{\vc{c}}$ and the parallelogram change in response. (You cannot change the red cross product vector $\color{red}{\vc{c}}$ directly.) The three-dimensional perspective of this graph may be easier to perceive if you keep the figure rotating by dragging it with your mouse.
Notice that the area of the parallelogram (and hence the magnitude of the cross product) go to zero as $\vc{a}$ and $\vc{b}$ approach parallel (where the term “parallel” also includes what you might think as anti-parallel). You can also verify that the applet demonstrates $\vc{b} \times \vc{a} = - \vc{a} \times \vc{b}$ and $\vc{a} \times \vc{a} = \vc{0}$, which are important properties of the cross product.
The geometric definition of the cross product is nice for understanding its properties. However, it's not too convenient for numerically calculating the cross product of vectors given in terms of their coordinates. For such calculations, you may want to have the formula for the cross product in terms of components. With the cross product formula in hand, you can make short work of any calculation, as illustrated by these examples of calculating cross products and areas of parallelograms.
Thread navigation
Vector algebra
- Previous: Dot product examples
- Next: The formula for the cross product
Math 2374
- Previous: Matrices and determinants
- Next: The formula for the cross product
Similar pages
- The formula for the cross product
- Cross product examples
- The dot product
- The formula for the dot product in terms of vector components
- Dot product examples
- The scalar triple product
- Scalar triple product example
- The zero vector
- The relationship between determinants and area or volume
- Multiplying matrices and vectors
- More similar pages