Applet: Discontinuous partial x derivative of a non-differentiable function
Applet loading
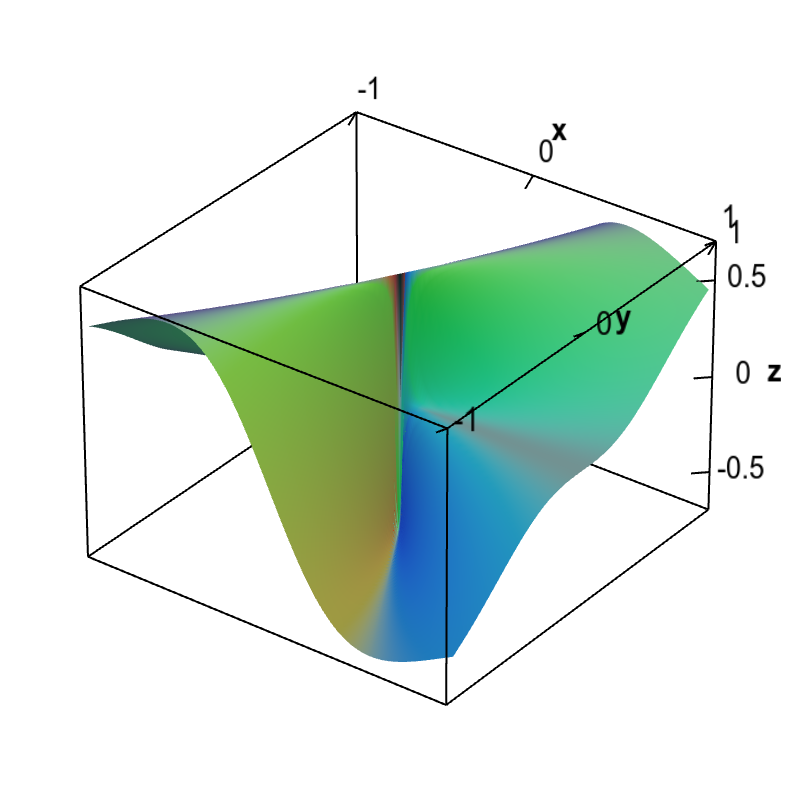
The graph of the partial derivative with respect to $x$ of a function $f(x,y)$ that is not differentiable at the origin is shown. The plot demonstrates that indeed $\pdiff{f}{x}(x,y)$ is discontinuous at the origin. The graph shows that $\pdiff{f}{x}(x,y)$ is both a large positive number (actually $3\sqrt{3}/8 \approx 0.65$) and a large negative number (actually $-3\sqrt{3}/8 \approx -0.65$) arbitrarily close to the origin. Hence, $\pdiff{f}{x}(x,y)$ jumps with a large discontinuity at the origin.
This function is \begin{align*} f(x,y) = \begin{cases} \displaystyle \frac{x^2y}{x^2+y^2} & \text{if } (x,y) \ne (0,0)\\ 0 & \text{if } (x,y) = (0.0). \end{cases} \end{align*} Its partial derivative with respect to $x$ is \begin{align*} \pdiff{f}{x}(x,y) &= \begin{cases} \displaystyle \frac{2 x y}{x^2+y^2}-\frac{2 x^3 y}{\left(x^2+y^2\right)^2} \ & \text{if } (x,y) \ne (0,0)\\ 0 & \text{if } (x,y) = (0.0). \end{cases} \end{align*} (One must use the limit definition to calculate the partial derivative at the origin.)
Plugging in $y=x\sqrt{3}$ gives $$\diff{f}{x}(x,x\sqrt{3})=\frac{3\sqrt{3}}{8}$$ and plugging in $y=-x\sqrt{3}$ gives $$\diff{f}{x}(x,-x\sqrt{3})=\frac{-3\sqrt{3}}{8}$$ as long as $x \ne 0$. Since both these values occur arbitrarily near the origin, $\pdiff{f}{x}(x,y)$ is discontinuous at the origin.
Applet file: discontinuous_partial_x_derivative_nondifferentiable_function.m
Applet links
This applet is found in the pages
General information about three.js applets
The applet was made using three.js and requires Javascript as well as a browser that supports WebGL. For most three.js applets, you can drag with the mouse to rotate the view, drag with the right button to pan, and zoom in/out with the mouse wheel. Many applets contain points that you can drag to change values of variables.