Non-differentiable functions must have discontinuous partial derivatives

According to the differentiability theorem, any non-differentiable function with partial derivatives must have discontinuous partial derivatives. (Otherwise, by the theorem, the function must be differentiable.) For one of the example non-differentiable functions, let's see if we can visualize that indeed these partial derivatives were the problem.

The function we'll examine is \begin{align*} f(x,y) = \begin{cases} \displaystyle \frac{x^2y}{x^2+y^2} & \text{if } (x,y) \ne (0,0)\\ 0 & \text{if } (x,y) = (0.0). \end{cases} \end{align*} Its graph is shown below.

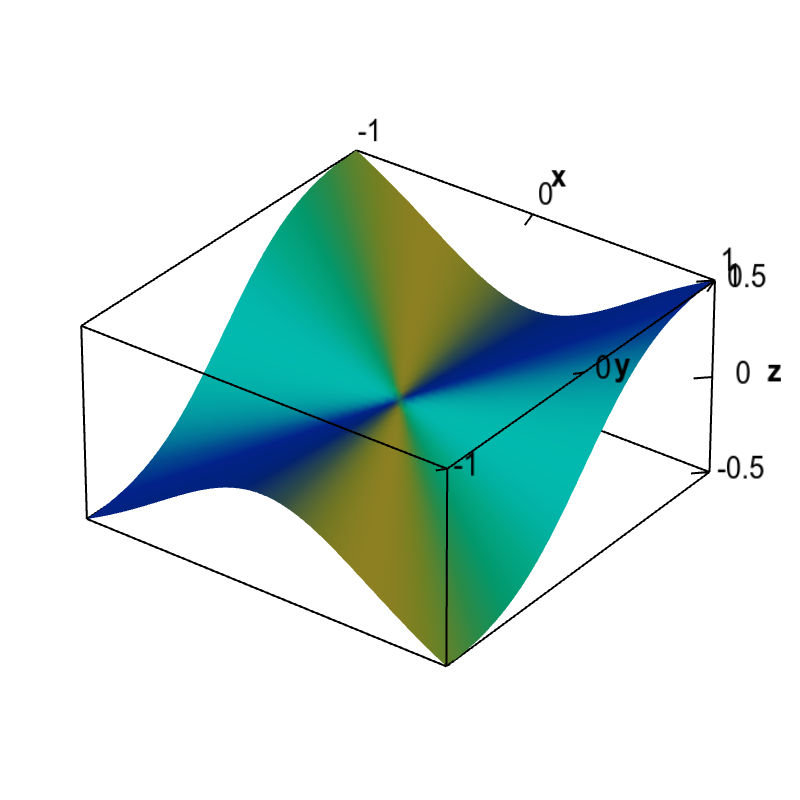
The Java applet did not load, and the above is only a static image representing one view of the applet. The applet was created with LiveGraphics3D. The applet is not loading because it looks like you do not have Java installed. You can click here to get Java.

Non-differentiable function with partial derivatives. The partial derivatives of this function $f(x,y)$ are zero at the origin, $\pdiff{f}{x}(0,0)=\pdiff{f}{y}(0,0)=0$. Therefore, the only possibility for a tangent plane would be a horizontal plane. However, since the slopes of this function coming to the origin along different directions are not zero, a horizontal plane cannot be tangent. We conclude that no tangent plane exists at the origin and this function is not differentiable there.

If you stare at the above plot, you might be able to convince yourself that the partial derivatives are discontinuous at the origin. For example, along the line $y=0$ but away from the origin, the slope $\pdiff{f}{y}$ is a positive constant (in fact $\pdiff{f}{y}(x,0)=1$ for $x \ne 0$). But, along the line $x=0$, the slope $\pdiff{f}{y}$ is zero. These two values clash at the origin, leading to a discontinuity of $\pdiff{f}{y}(x,y)$ at the origin $(0,0)$. The partial derivative with respect to $x$, $\pdiff{f}{x}$, on the other hand, switches sign as you cross the line $x=0$. As you approach the origin, the switch happens faster, eventually switching with an instantaneous jump at the origin.

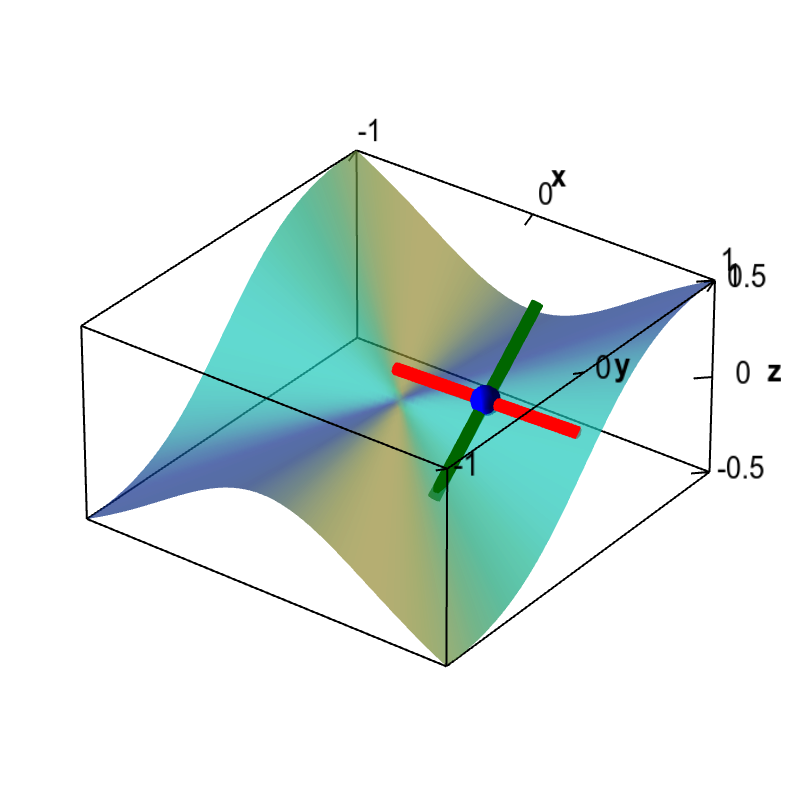
The following applet allows you visualize the partial derivatives as slopes. If you drag the point around the origin, you will see that the slopes jump, reflecting the fact that they are discontinuous.

The Java applet did not load, and the above is only a static image representing one view of the applet. The applet was created with LiveGraphics3D. The applet is not loading because it looks like you do not have Java installed. You can click here to get Java.

Slopes illustrating the discontinuous partial derivatives of a non-differentiable function. Although this function, shown as a mesh plot, has partial derivatives defined everywhere, the partial derivatives are discontinuous at the origin. The colored line segments around the movable red point illustrate the partial derivatives. The slope of the dark blue line is $\pdiff{f}{x}$ while the slope of the light green line is $\pdiff{f}{y}$. As you move the point near the origin using the mouse, the slopes will change sharply, reflecting the fact that they are discontinuous around the origin. Since the function is not differentiable at the origin, i.e., there is no tangent plane at the origin, we know from the differentiability theorem that the partial derivatives must not be continuous there.

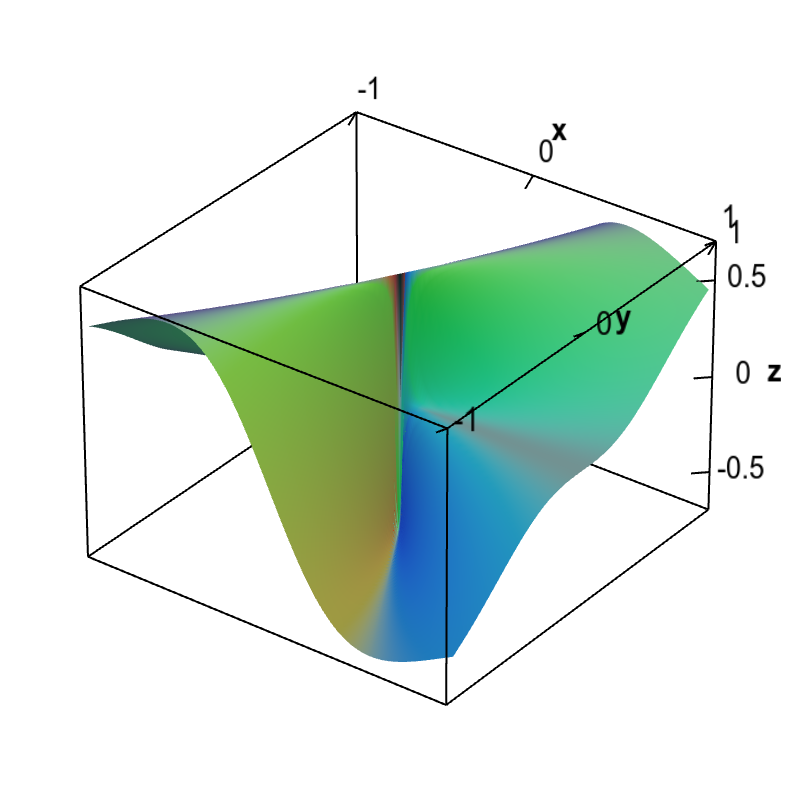
An even better demonstration that the partial derivatives are indeed discontinuous is a plot of the partial derivative. Below is a plot of partial derivative of $f(x,y)$ with respect to $x$.

The Java applet did not load, and the above is only a static image representing one view of the applet. The applet was created with LiveGraphics3D. The applet is not loading because it looks like you do not have Java installed. You can click here to get Java.

Discontinuous partial x derivative of a non-differentiable function. The graph of the partial derivative with respect to $x$ of a function $f(x,y)$ that is not differentiable at the origin is shown. The plot demonstrates that indeed $\pdiff{f}{x}(x,y)$ is discontinuous at the origin. The graph shows that $\pdiff{f}{x}(x,y)$ is both a large positive number (actually $3\sqrt{3}/8 \approx 0.65$) and a large negative number (actually $-3\sqrt{3}/8 \approx -0.65$) arbitrarily close to the origin. Hence, $\pdiff{f}{x}(x,y)$ jumps with a large discontinuity at the origin.

How can we be 100% sure that the $\pdiff{f}{x}$ is discontinuous at the origin? Of course, such visualization are imperfect, and you never know if you are being mislead. But, we can back up the picture with a calculation. The partial derivatives of $f(x,y)$ are \begin{align*} \pdiff{f}{x}(x,y) &= \begin{cases} \displaystyle \frac{2 x y}{x^2+y^2}-\frac{2 x^3 y}{\left(x^2+y^2\right)^2} \ & \text{if } (x,y) \ne (0,0)\\ 0 & \text{if } (x,y) = (0.0). \end{cases} \\ \pdiff{f}{y}(x,y) &= \begin{cases} \displaystyle \frac{x^2}{x^2+y^2}-\frac{2 x^2 y^2}{\left(x^2+y^2\right)^2} \ & \text{if } (x,y) \ne (0,0)\\ 0 & \text{if } (x,y) = (0.0). \end{cases}. \end{align*} To calculate the partial derivatives away from the origin, we just used the usual rules for differentiation. At the origin, we had to use the limit definition of partial derivatives, as shown on another page.

It's easy to see that the partial derivatives are zero along the $x$ and $y$ axes, as setting either $x=0$ or $y=0$ makes all the above expressions disappear. Focusing on the $x$-derivative, you can show that setting $y=x\sqrt{3}$ leads to a positive constant, $$\pdiff{f}{x}(x,x\sqrt{3}) = \frac{3\sqrt{3}}{8} \approx 0.65,$$ as long as you stay away from the origin. On the other hand, setting $y=-x\sqrt{3}$ lead to a negative constant $$\pdiff{f}{x}(x,-x\sqrt{3}) = -\frac{3\sqrt{3}}{8} \approx -0.65.$$

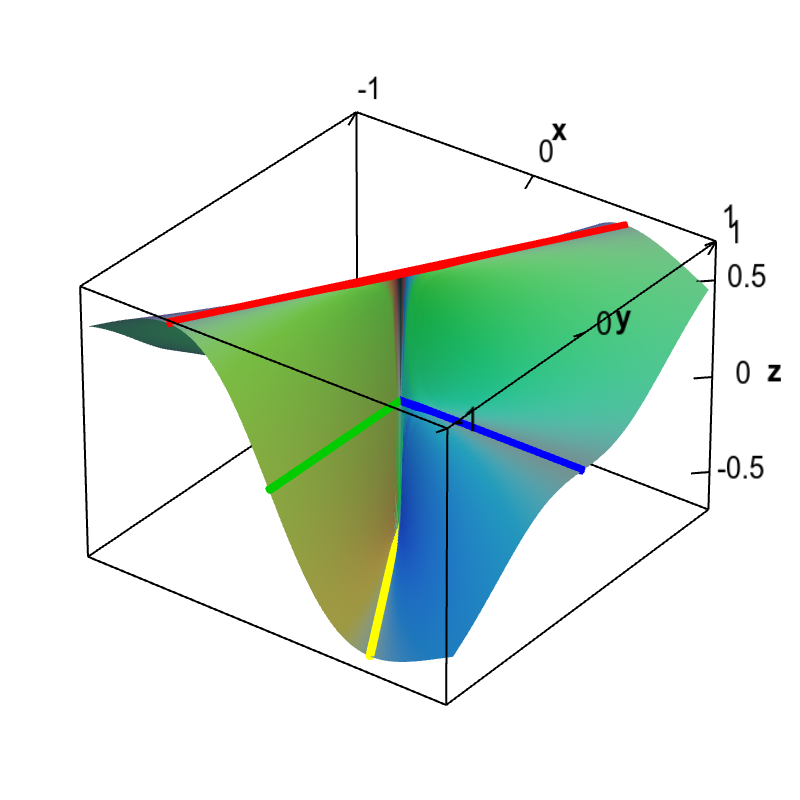
These four lines along which $\pdiff{f}{x}(x,y)$ is constant are overlaid on the graph shown below. Since all the lines go to the origin, they are a convincing demonstration that within any neighborhood of the origin, $\pdiff{f}{x}(x,y)$ takes on the values $0$, $\frac{3\sqrt{3}}{8}$, and $-\frac{3\sqrt{3}}{8}$. We've obtained different values for the limit of $\pdiff{f}{x}(x,y)$ along paths going to the origin, demonstrating that $\pdiff{f}{x}(x,y)$ is discontinuous at the origin.

The Java applet did not load, and the above is only a static image representing one view of the applet. The applet was created with LiveGraphics3D. The applet is not loading because it looks like you do not have Java installed. You can click here to get Java.

Lines demonstrating the discontinuity of the partial x derivative of a non-differentiable function. This graph shows the partial derivative with respect to $x$ of a function $f(x,y)$ that is not differentiable at the origin. The discontinuity of $\pdiff{f}{x}(x,y)$ is demonstrated by overlaying lines along which $\pdiff{f}{x}$ is constant. Along the blue line of the $x$-axis and the green line of the $y$ axis, $\pdiff{f}{x}$ is zero. However, along the line $y=x\sqrt{3}$ (in red), $\pdiff{f}{x}=3\sqrt{3}/8 \approx 0.65$, and along the line $y=-x\sqrt{3}$ (in yellow), $\pdiff{f}{x}=-3\sqrt{3}/8 \approx -0.65$. Since within any neighborhood of the origin, $\pdiff{f}{x}(x,y)$ takes on these different values, the partial derivative $\pdiff{f}{x}(x,y)$ is discontinuous at the origin.

It's a good thing that the partial derivatives of $f(x,y)$ are discontinuous at the origin. Otherwise, since $f(x,y)$ is non-differentiable at the origin, it would have contradicted the differentiability theorem. Be sure to keep your logic straight, though, as the differentiability theorem does not imply that all differentiable functions have continuous partial derivatives, as shown by this example.