Applet: Double integral Riemann sum
Applet loading
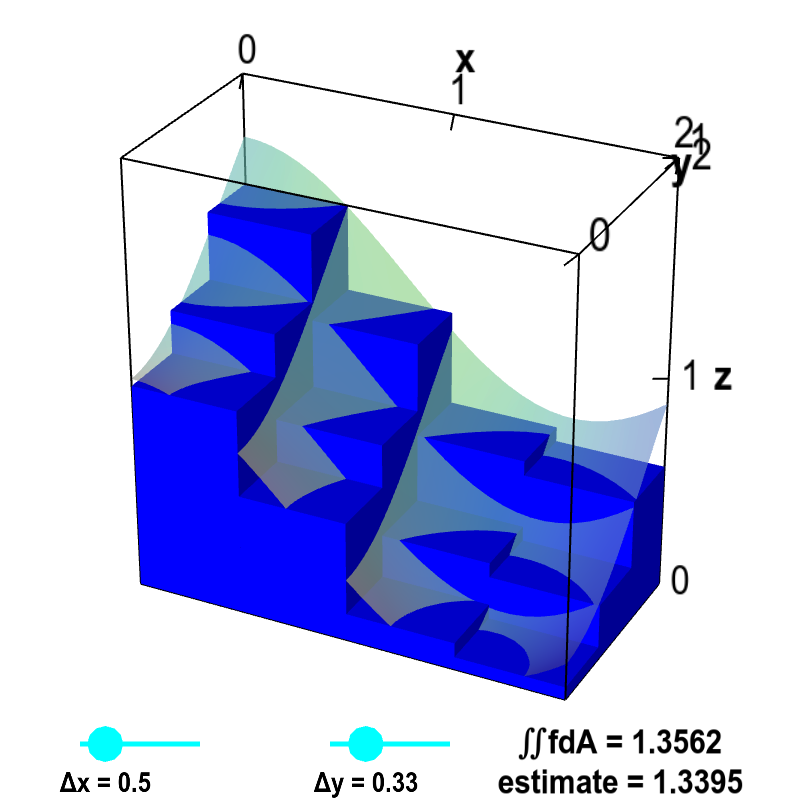
The volume of the small boxes illustrates a Riemann sum approximating the volume under the graph of $z=f(x,y)$, shown as a transparent surface. The surface is the graph of the function $f(x,y)=\cos^2 x + \sin^2 y$. The volume is computed over the region $D$ defined by $0 \le x \le 2$ and $0 \le y \le 1$. Therefore, the actual volume is the double integral $\iint_D f\,dA$. The volume of the boxes is $$\sum_{i,j} f(x_{i},y_{j})\Delta x \Delta y$$ where $x_i$ is the midpoint of the $i$th interval along the $x$-axis and $y_j$ is the midpoint of the $j$th interval along the $y$-axis. Drag the points on the sliders to change $\Delta x$ and $\Delta y$ as well as the number of intervals along each axis. As $\Delta x$ and $\Delta y$ approach zero, the volume of the boxes (labeled as “estimate”) approaches the actual volume of the integral $\iint_D f\,dA$.
Applet links
This applet is found in the pages
General information about three.js applets
The applet was made using three.js and requires Javascript as well as a browser that supports WebGL. For most three.js applets, you can drag with the mouse to rotate the view, drag with the right button to pan, and zoom in/out with the mouse wheel. Many applets contain points that you can drag to change values of variables.