Math Insight

Double integrals as volume

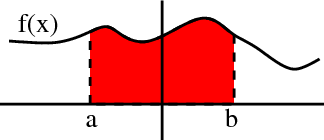
You are probably familiar that in one-variable calculus, the integral $\int_a^b f(x)dx$ for positive $f(x)$ can be interpreted as the area under the curve $f(x)$ over the interval $[a,b]$.

The integral is the area between the curve $f(x)$ and the $x$-axis.

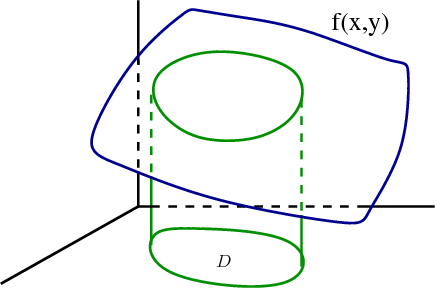
In the same way, the double integral $\iint_\dlr f(x,y)\,dA$ of positive $f(x,y)$ can be interpreted as the volume under the surface $z=f(x,y)$ over the region $\dlr$. Imagine that the blue object below is the surface $z=f(x,y)$ floating above the $xy$-plane. The double integral $\iint_\dlr f(x,y)\,dA$ can be interpreted as the volume between the surface $z=f(x,y)$ and the $xy$-plane, i.e, the “cylinder” above the region $\dlr$.

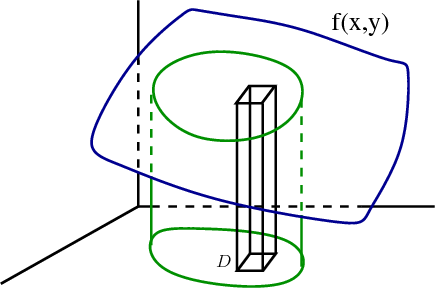
You can also see this from the Riemann sum approximating the integral \begin{align*} \sum_{i,j} f(x_{ij}, y_{ij}) \Delta x \Delta y \end{align*} Each term in the Riemann sum is the volume of a thin box with base $\Delta x \times \Delta y$ and height $f(x_{ij},y_{ij})$.

Hence, the total Riemann sum approximates the volume under the surface by the volume of a bunch of these thin boxes. In the limit as $\Delta x, \Delta y \to 0$, we obtain the total volume under the surface over the region $\dlr$, i.e., $\iint_\dlr f(x,y)\, dA$.

The below applet illustrates how the volume of the boxes approaches the area under the surface as $\Delta x$ and $\Delta y$ decrease to zero.

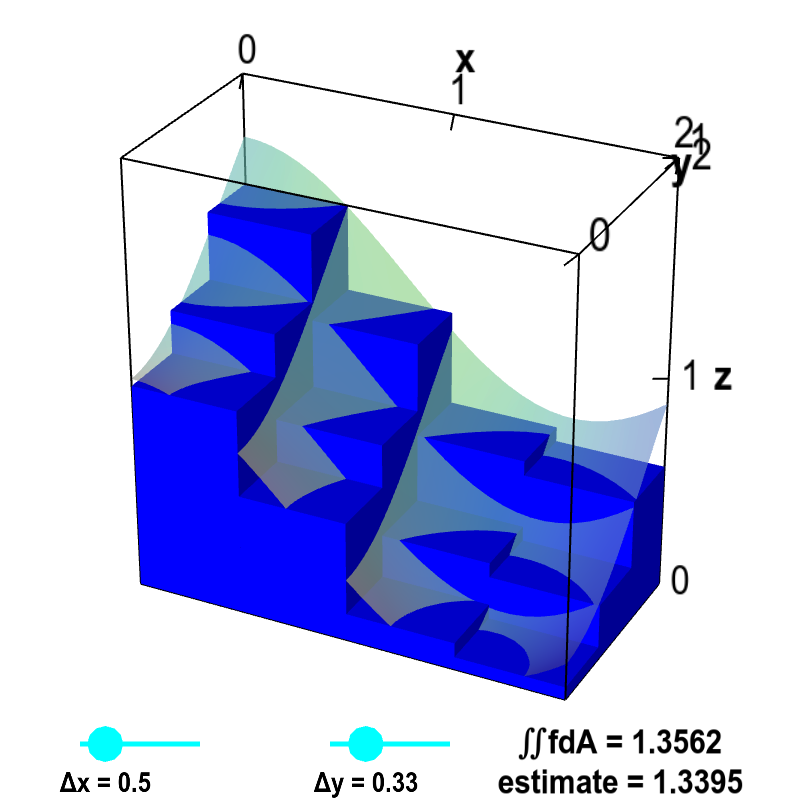
Applet loading

Double integral Riemann sum. The volume of the small boxes illustrates a Riemann sum approximating the volume under the graph of $z=f(x,y)$, shown as a transparent surface. The surface is the graph of the function $f(x,y)=\cos^2 x + \sin^2 y$. The volume is computed over the region $D$ defined by $0 \le x \le 2$ and $0 \le y \le 1$. Therefore, the actual volume is the double integral $\iint_D f\,dA$. The volume of the boxes is $$\sum_{i,j} f(x_{i},y_{j})\Delta x \Delta y$$ where $x_i$ is the midpoint of the $i$th interval along the $x$-axis and $y_j$ is the midpoint of the $j$th interval along the $y$-axis. Drag the points on the sliders to change $\Delta x$ and $\Delta y$ as well as the number of intervals along each axis. As $\Delta x$ and $\Delta y$ approach zero, the volume of the boxes (labeled as “estimate”) approaches the actual volume of the integral $\iint_D f\,dA$.

More information about applet.

If $f(x,y) > g(x,y)$ can you see how the double integral \begin{align*} \iint_\dlr (f(x,y)-g(x,y))\,dA \end{align*} is the volume between the surface $z=f(x,y)$ and the surface $z=g(x,y)$?

The below examples assume you know how to write double integrals as interated integrals.

Example 1

Calculate the volume under the surface $z=3+x^2-2y$ over the region $\dlr$ defined by $0 \le x \le 1$ and $-x \le y \le x$.

Solution: The volume $V$ is the double integral of $3+x^2-2y$ over $\dlr$. \begin{align*} V &= \iint_{\dlr} (3+x^2-2y)dx\,dy\\ &= \int_0^1 \int_{-x}^x (3+x^2-2y) dy\, dx\\ &= \int_0^1 \left(3y+x^2y-y^2\Big|_{y=-x}^{y=x}\right) dx\\ &= \int_0^1 (6x+2x^3) dx\\ &= 3x^2 +\frac{1}{2}x^4 \Big|_0^1 = 3\frac{1}{2} \end{align*}

Example 2

Calculate the volume between the surfaces $z=f(x,y)=3-x^2-y^2$ and the surface $z=g(x,y)=2x^2+2y^2$.

Solution: At the origin, $f$ is above $g$, since $f(0,0)=3$ and $g(0,0)=0$. As one moves away from the origin, $f$ gets large and negative, while $g$ gets large and positive. Therefore, $f$ and $g$ must cross somewhere, and the finite volume between $f$ and $g$ is the integral of $f-g$ over the region where $f > g$.

We can calculate where the surfaces cross by setting $f=g$. This occurs when \begin{align*} f(x,y) &= g(x,y)\\ 3-x^2-y^2 &= 2x^2+2y^2\\ 3 &= 3x^2+3y^2\\ 1 &= x^2+y^2. \end{align*} The curve where the surfaces cross is the unit circle, and the region $\dlr$ over which we must integrate $f-g$ is the unit disk $x^2+y^2 \le 1$.

The volume $V$ is \begin{align*} V &=\iint_{\dlr} (f(x,y)-g(x,y)) dx\,dy = \iint_{\dlr} (3 - 3x^2-3y^2)dx \, dy. \end{align*}

This integral is very simple to calculate if you know how to change variables to polar coordinates. (If you don't yet know how to do this, you can still calculate the integral if you are good at doing integrals, but it gets pretty ugly. We'll show the procedure below.)

In polar coordinates, the unit disk is the region $0 \le r \le 1$, $0 \le \theta \le 2\pi$. Including the extra factor of $r$ from the change of variables, the integral becomes \begin{align*} V &= \iint_{\dlr} (3 - 3x^2-3y^2)dx \, dy\\ &= \int_0^{2\pi} \int_0^1 (3 - 3r^2)r\,dr\,d\theta\\ &= \int_0^{2\pi} \left(\frac{3}{2}r^2 - \frac{3}{4}r^4 \Big|_{r=0}^{r=1}\right)d\theta\\ &= \int_0^{2\pi} \frac{3}{4} d\theta = \frac{3\pi}{2}. \end{align*}

If you don't know how to change variables to polar coordinates, you can do the integration over disk by writing it as $-1 \le x \le 1$, $-\sqrt{1-x^2} \le y \le \sqrt{1-x^2}$. As you can see below, you'll have to do a trigonometric substitution $x=\sin\theta$ as well as other trigonometric identities to evaluate the integral. With this trigonometric substitution, the range of $\theta$ is $-\pi/2 \le \le \pi/2$ so that $x=\sin\theta$ ranges from $-1 \le x \le 1$. Rather than explain every step, we'll just show some of the intermediate calculations. You won't want to try to follow this anyway unless you are already skilled at integration.

Here's the calculation: \begin{align*} V &= \iint_{\dlr} (3 - 3x^2-3y^2)dx \, dy\\ &= \int_{-1}^1\int_{-\sqrt{1-x^2}}^{\sqrt{1-x^2}}(3 - 3x^2-3y^2)dy\,dx\\ &= \int_{-1}^1(3y - 3x^2y-y^3)\Big|_{y=-\sqrt{1-x^2}}^{y=\sqrt{1-x^2}} dx\\ &=\int_{-1}^1(6\sqrt{1-x^2}-6x^2\sqrt{1-x^2}-2(1-x^2)^{3/2})dx\\ &=\int_{-\pi/2}^{\pi/2}(6\sqrt{1-\sin^2\theta}-6\sin^2\theta\sqrt{1-\sin^2\theta}-2(1-\sin^2\theta)^{3/2})\cos \theta d\theta\\ &=\int_{-\pi/2}^{\pi/2}(6\cos\theta-6\sin^2\theta\cos\theta-2\cos^3\theta)\cos \theta d\theta\\ &=\int_{-\pi/2}^{\pi/2}4\cos^4\theta d\theta\\ &=\int_{-\pi/2}^{\pi/2}\left(\frac{3}{2}+2\cos 2\theta+\frac{1}{2}\cos 4\theta\right)d\theta\\ &=\left[\frac{3}{2}\theta+\sin 2\theta+\frac{1}{8}\sin 4\theta\right]_{-\pi/2}^{\pi/2} =\frac{3\pi}{2}. \end{align*}