Applet: Macroscopic and microscopic circulation in three dimensions
Applet loading
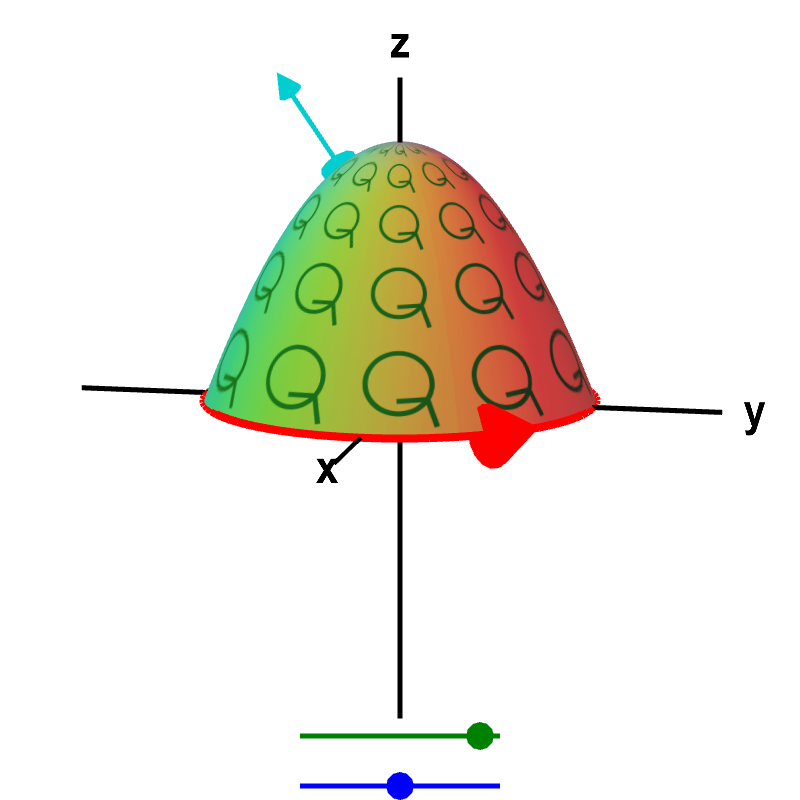
The relationship between the macroscopic circulation of a vector field $\dlvf$ around a curve (red boundary of surface) and the microscopic circulation of $\dlvf$ (illustrated by small green circles) along a surface in three dimensions must hold for any surface whose boundary is the curve. No matter which surface you choose (change by dragging the green point on the top slider), the total microscopic circulation of $\dlvf$ along the surface must equal the circulation of $\dlvf$ around the curve (We assume that the vector field $\dlvf$ is defined everywhere on the surface.)
You can change the curve to a more complicated shape by dragging the blue point on the bottom slider, and the relationship between the macroscopic and total microscopic circulation still holds.
The definition of microscopic circulation depends on the orientation of the surface, which is specified by the choice of the normal vector (shown in cyan). The definition of the macroscopic circulation depends on the orientation of the curve, which is specified by the red arrow on the curve. Since the orientation of these normal vectors have the proper relationship for Stokes' theorem to apply, the macroscopic and microscopic circulation values will match.
Applet links
This applet is found in the pages
- How to determine if a vector field is conservative
- The idea behind Stokes' theorem
- Proper orientation for Stokes' theorem
General information about three.js applets
The applet was made using three.js and requires Javascript as well as a browser that supports WebGL. For most three.js applets, you can drag with the mouse to rotate the view, drag with the right button to pan, and zoom in/out with the mouse wheel. Many applets contain points that you can drag to change values of variables.