The idea behind Stokes' theorem
Stokes' theorem is a generalization of Green's theorem from circulation in a planar region to circulation along a surface.
Green's theorem states that, given a continuously differentiable two-dimensional vector field $\dlvf$, the integral of the “microscopic circulation” of $\dlvf$ over the region $\dlr$ inside a simple closed curve $\dlc$ is equal to the total circulation of $\dlvf$ around $\dlc$, as suggested by the equation \begin{align*} \dlint = \iint_\dlr \text{“microscopic circulation of $\dlvf$” } dA. \end{align*} We often write that $\dlc = \partial \dlr$ as fancy notation meaning simply that $\dlc$ is the boundary of $\dlr$. Green's theorem requires that $\dlc = \partial \dlr$.
The “microscopic circulation” in Green's theorem is captured by the curl of the vector field and is illustrated by the green circles in the below figure.
Green's theorem applies only to two-dimensional vector fields and to regions in the two-dimensional plane. Stokes' theorem generalizes Green's theorem to three dimensions. For starters, let's take our above picture and simply embed it in three dimensions. Then, our curve $\dlc$ becomes a curve in the $xy$-plane, and our region $\dlr$ becomes a surface $\dls$ in the $xy$-plane whose boundary is the curve $\dlc$. Even though $\dls$ is now a surface, we still use the same notation as $\partial$ for the boundary. The boundary $\partial \dls$ of the surface $\dls$ is a closed curve, and we require that $\partial \dls = \dlc$.
The next question is what the microscopic circulation along a surface should be. For Green's theorem, we found that \begin{align*} \text{“microscopic circulation”} = (\curl \dlvf) \cdot \vc{k}, \end{align*} (where $\vc{k}$ is the unit-vector in the $z$-direction). We wanted the component of the curl in the $\vc{k}$ direction because this corresponded to microscopic circulation in the $xy$-plane. Similarly, for a surface, we will want the microscopic circulation along the surace. This corresponds to the component of the curl that is perpendicular to the surface, i.e, \begin{align*} \text{“microscopic circulation”} = (\curl \dlvf) \cdot \vc{n}, \end{align*} where $\vc{n}$ is a unit normal vector to the surface. You can see this using the right-hand rule. If you point the thumb of your right hand perpendicular to a surface, your fingers will curl in a direction corresponding to circulation parallel to the surface.
In summary, to go from Green's theorem to Stoke's theorem, we've made two changes. First, we've changed the line integral living in two dimensions (Green's theorem) to a line integral living in three dimensions (Stokes' theorem). Second, we changed the double integral of $\curl \dlvf \cdot \vc{k}$ over a region $\dlr$ in the plane (Green's theorem) to a surface integral of $\curl \dlvf \cdot \vc{n}$ over a surface floating in space (Stokes' theorem). The required relationship between the curve $\dlc$ and the surface $\dls$ (Stokes' theorem) is identical to the relationship between the curve $C$ and the region $\dlr$ (Green's theorem): the curve $\dlc$ must be the boundary $\partial \dlr$ of the region or the boundary $\partial \dls$ of the surface.
We write Stokes' theorem as: \begin{align*} \dlint = \ssint{\dls}{\curl \dlvf \cdot \vc{n}} = \sint{\dls}{\curl \dlvf} \end{align*} (Recall that a surface integral of a vector field is the integral of the component of the vector field perpendicular to the surface.) We see that the integral on the right is the surface integral of the vector field $\curl \dlvf$. Stokes theorem says the surface integral of $\curl \dlvf$ over a surface $\dls$ (i.e., $\sint{\dls}{\curl \dlvf}$) is the circulation of $\dlvf$ around the boundary of the surface (i.e., $\dlint$ where $\dlc = \partial \dls$ ).
Once we have Stokes' theorem, we can see that the surface integral of $\curl \dlvf$ is a special integral. The integral cannot change if we can change the surface $\dls$ to any surface as long as the boundary of $\dls$ is still the curve $\dlc$. It cannot change because it still must be equal to $\dlint$, which doesn't change if we don't change $\dlc$. (In analogy of how the gradient $\nabla f$ is a path-independent vector field, you could say that $\curl \dlvf$ is “surface independent” vector field, but we don't usually use that term.)
For example, staring with a planar surface such as sketched above, we see that the surface $\dls$ doesn't have to be the flat surface inside $\dlc$. We can bend and stretch $\dls$, and the above formula is still true. In the below applet, you can move the green point on the top slider to change the surface $\dls$. For any of those surfaces, the integral of the “microscopic circulation” $\curl \dlvf$ over that surface will be the total circulation $\dlint$ of $\dlvf$ around the curve $\dlc$ (shown in red). The important restriction is that the boundary of the surface $\dls$ is still the curve $\dlc$.
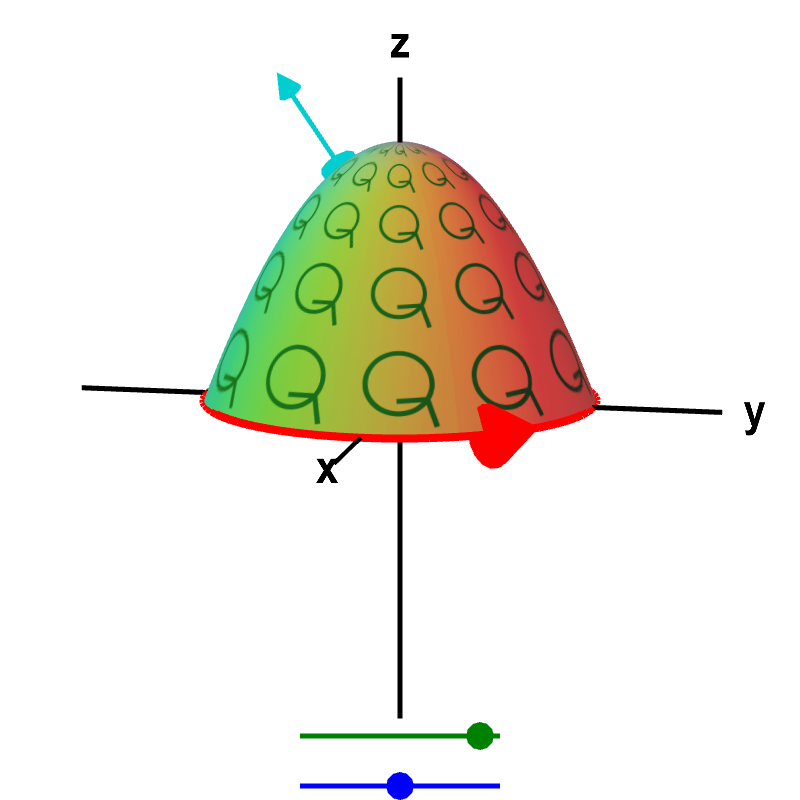
Applet loading
Macroscopic and microscopic circulation in three dimensions. The relationship between the macroscopic circulation of a vector field $\dlvf$ around a curve (red boundary of surface) and the microscopic circulation of $\dlvf$ (illustrated by small green circles) along a surface in three dimensions must hold for any surface whose boundary is the curve. No matter which surface you choose (change by dragging the green point on the top slider), the total microscopic circulation of $\dlvf$ along the surface must equal the circulation of $\dlvf$ around the curve. (We assume that the vector field $\dlvf$ is defined everywhere on the surface.) You can change the curve to a more complicated shape by dragging the blue point on the bottom slider, and the relationship between the macroscopic and total microscopic circulation still holds. The surface is oriented by the shown normal vector (moveable cyan arrow on surface), and the curve is oriented by the red arrow.
Stokes' theorem allows us to do even more. We don't have to leave the curve $\dlc$ sitting in the $xy$-plane. We can twist and turn $\dlc$ as well. If $\dls$ is a surface whose boundary is $\dlc$ (i.e., if $\dlc = \partial \dls$), it is still true that \begin{align*} \dlint = \sint{\dls}{\curl \dlvf}. \end{align*} For example, in the above applet, you can also move the blue point on the bottom slider to change the curve $\dlc$. The surface $\dls$ also changes as you change $\dlc$, since its boundary has to be $\dlc$.
Note that moving the green point on the top slider does not change the value of either integral in the above formulas. Since the curve $\dlc$ does not change, the left line integral doesn't change, which means the value of the right surface integral cannot change. On the other hand, moving the blue point on the bottom slider does change the values of the integrals since the curve $\dlc$ changes. The important point is that, even in this case, the left line integral and the right surface integral are always equal.
There is one more subtlety that you have to get correct, or else you'll may be off by a sign. You need to orient the surface and boundary properly. The cyan normal vector to the surface and the orientation of the curve (shown by red arrow) in the above applet are chosen with the proper relative orientations so that Stokes' theorem applies.
You can read some examples here.
Thread navigation
Multivariable calculus
- Previous: Green's theorem with multiple boundary components
- Next: Proper orientation for Stokes' theorem
Math 2374
Notation systems
Similar pages
- Proper orientation for Stokes' theorem
- Stokes' theorem examples
- The idea behind Green's theorem
- The definition of curl from line integrals
- Calculating the formula for circulation per unit area
- The idea of the curl of a vector field
- Subtleties about curl
- The components of the curl
- Line integrals as circulation
- A path-dependent vector field with zero curl
- More similar pages

