Applet: Non-differentiable function with partial derivatives
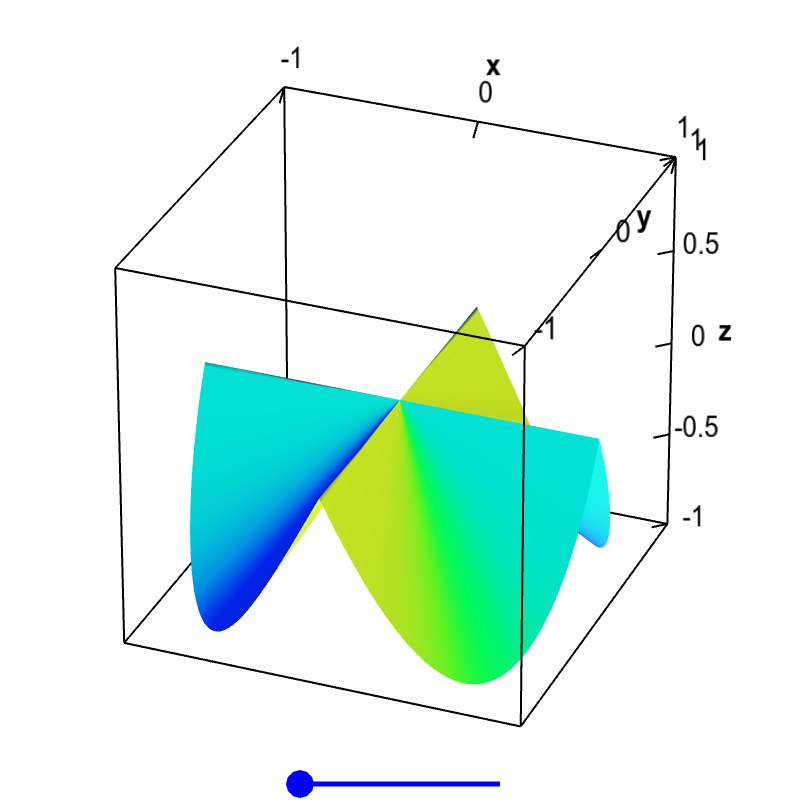
Applet loading
The partial derivatives of this function $f(x,y)$ exist at the origin, $\pdiff{f}{x}(0,0)=0$ and $\pdiff{f}{y}(0,0)=0$, as the function is constant along the $x$ and $y$ axis, $f(x,0)=f(0,y)=0$. However, the slopes coming into the origin from other directions are non-zero. If there were a tangent plane at the origin, it would have to be the horizontal plane $z=0$, as that is the only plane that would be tangent along the $x$ and $y$ directions. Clearly, the slopes would not match in other directions, so this plane is not tangent. Therefore, there is no tangent plane at $\vc{a}=(0,0)$, and the function is not differentiable there. You can drag the blue point on the slider to remove the folds in the surface, but that does not change the partial derivatives at the origin. The wrinkle at the origin is enough to make the function non-differentiable.
Applet links
This applet is found in the pages
General information about three.js applets
The applet was made using three.js and requires Javascript as well as a browser that supports WebGL. For most three.js applets, you can drag with the mouse to rotate the view, drag with the right button to pan, and zoom in/out with the mouse wheel. Many applets contain points that you can drag to change values of variables.