Subtleties of differentiability in higher dimensions
The definition of differentiability
The definition of differentiability in higher dimensions looks fairly intimidating at first glance. For this reason, we suggest beginning by reading the page about the intuition behind this definition. We repeat the definition from the end of that page.
Definition: The function $\vc{f}: \R^n \to \R^m$ is differentiable at the point $\vc{a}$ if there exists a linear transformation $\vc{T}: \R^n \to \R^m$ that satisfies the condition $$\lim_{\vc{x} \to \vc{a}} \frac{\| \vc{f}(\vc{x})-\vc{f}(\vc{a}) - \vc{T}(\vc{x}-\vc{a})\|}{\|\vc{x}-\vc{a}\|} = 0.$$
The $m \times n$ matrix associated with the linear transformation $\vc{T}$ is the matrix of partial derivatives, which we denote by $\jacm{f}(\vc{a})$. We can refer to $\jacm{f}(\vc{a})$ as the total derivative (or simply the derivative) of $\vc{f}$.
The trouble with limits in higher dimensions
The differentiabililty definition is based on the limit $\vc{x} \to \vc{a}$. In order for this limit to exist, we have to get the same result, no matter the route $\vc{x}$ takes on its way to $\vc{a}$. If we find two routes that give different values for this limit, then we can conclude the limit does not exist. In many of the subtle cases where a function fails to be differentiable, one can find linear transformations $\vc{T}$ where $$\frac{\| \vc{f}(\vc{x})-\vc{f}(\vc{a}) - \vc{T}(\vc{x}-\vc{a})\|}{\|\vc{x}-\vc{a}\|}$$ does go to zero when $\vc{x}$ approaches $\vc{a}$ along some routes, but it does not go to zero when $\vc{x}$ approaches $\vc{a}$ along other routes. Don't make the mistake concluding a function must be differentiable after checking that you get zero along just a few paths of $\vc{x} \to \vc{a}$.
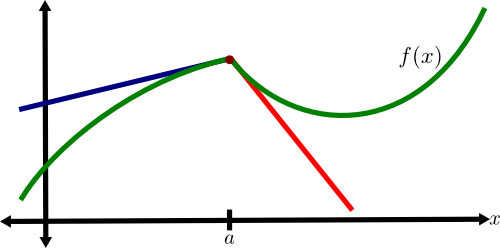
For a scalar-valued function of one variable, $f(x)$, checking that this limit is zero isn't too difficult. On the real line, there are only two routes for $x$ to get to $a$. It can approach $a$ from above or from below. If we find a candidate tangent line $$L(x)=f(a)+T(x-a)=f(a)+m(x-a)$$ where the upper and lower limits are both zero, then we can conclude that we really found a tangent line and the function is differentiable.
On the other hand, as pictured below, we may be able to find one candidate tangent line (in blue) where the limit is zero from the left but not the right. And we may find a second candidate tangent line (in red) where the limit is zero from the right and not the left. But in this case, it easy to see what is happening and to identify the kink in $f(x)$ that makes it non-differentiable at $x=a$.
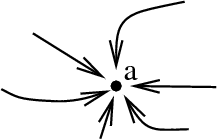
Increasing the number of dimensions to two or more makes a limit become much more complicated. Now, one has to consider all the possible paths $\vc{x}$ could take to the point $\vc{a}$, such as the ones illustrated below for the case of two dimensions. The challenge is the fact that there are an infinite number of such paths, and one needs to get the same limiting value on all these paths in order for the limit to exist.
Understanding the differentiability condition in two dimensions
To develop an intuition of the subtle ways in which the differentiability condition could be violated, it's enough to stick with scalar-valued functions of two variables, $f: \R^2 \to \R$. In this case, we can plot the graph of $f$ as a surface, and we understand that the linear approximation $$L(\vc{x}) = f(\vc{a}) + T(\vc{x}-\vc{a})$$ is a tangent plane.
We will also leave our formal definition of differentiability aside, and just focus on the geometry of the tangent plane. You can gather intuition about the correspondence between this definition and tangent planes in the page on the definition of differentiability. The differentiability definition requires the tangent plane to be tangent to the graph along any path of $\vc{x}$ that goes to the point $\vc{a}$.
The important consequence of this fact is that the existence of a derivative is much stronger than the existence of partial derivatives. Partial derivatives involve the limit of $\vc{f}$ only along directions parallel to the coordinate axes (in the above picture, such limits would be arrows coming straight in from the left, right, top, and bottom).
If a function varies smoothly along the paths coming into $\vc{a}$ from the positive and negative $x$ directions, the partial derivative with respect to $x$ at the point $\vc{a}$ will exist. If a function varies smoothly along the paths coming in from the positive and negative $y$ directions, the partial derivative with respect to $y$ at the point $\vc{a}$ will exist.
But just because the function behaves “nicely” along those four directions, it doesn't mean it behaves nicely along every path coming into $\vc{a}$.
For example, look at the following surface. At the origin (i.e., $\vc{a}=(0,0)$), the partial derivatives exist and are zero. (If one moves in the positive or negative $x$ or $y$ direction, the function is constant.)
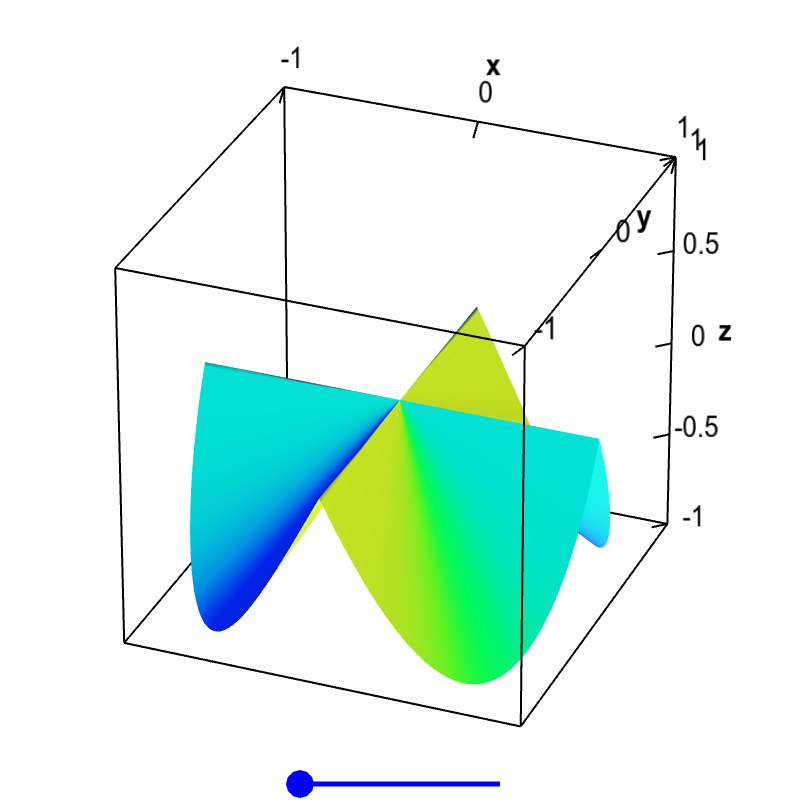
Applet loading
Non-differentiable function with partial derivatives. The partial derivatives of this function $f(x,y)$ exist at the origin, $\pdiff{f}{x}(0,0)=0$ and $\pdiff{f}{y}(0,0)=0$, as the function is constant along the $x$ and $y$ axis, $f(x,0)=f(0,y)=0$. However, the slopes coming into the origin from other directions are non-zero. If there were a tangent plane at the origin, it would have to be the horizontal plane $z=0$, as that is the only plane that would be tangent along the $x$ and $y$ directions. Clearly, the slopes would not match in other directions, so this plane is not tangent. Therefore, there is no tangent plane at $\vc{a}=(0,0)$, and the function is not differentiable there. You can drag the blue point on the slider to remove the folds in the surface, but that does not change the partial derivatives at the origin. The wrinkle at the origin is enough to make the function non-differentiable.
However, if you approach the origin from a path coming from any other direction, the slope of the path will be nonzero. You'll be climbing uphill as you reach the origin (or possibly going downhill if you changed the surface to remove the folds).
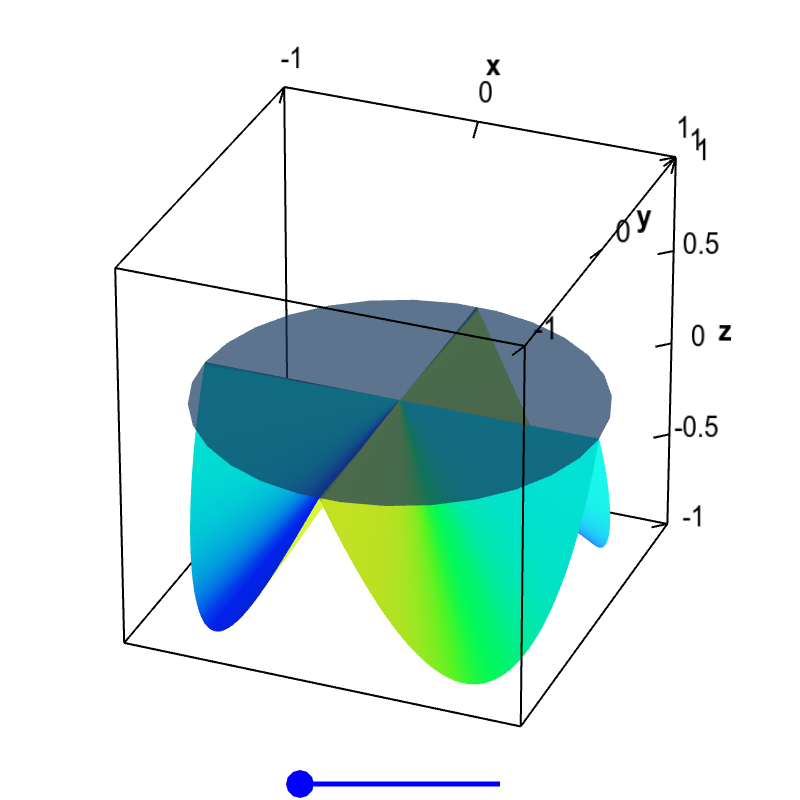
If the function were differentiable at the origin, it would have a tangent plane at the origin. If a tangent plane existed, the slopes would have to match the partial derivatives. In this case, since the partial derivatives are zero, the only option for the tangent plane is the horizontal plane, as shown below. Clearly this plane is not a tangent plane, as it is not tangent to paths approaching the origin from all directions. This surface is a graph of a function that has partial derivatives at the origin but is not differentiable at the origin.
Applet loading
Non-differentiable function with partial derivatives and no tangent plane. Since the partial derivatives of this function $f(x,y)$ exist and are zero at the origin, the only possible candidate for a tangent plane is the horizontal plane $z=0$ shown here. Although this plane is tangent along the $x$ and $y$ directions, the slopes of the function clearly do not match in other directions. Therefore, there is no tangent plane at $\vc{a}=(0,0)$, and the function is not differentiable there. You can drag the blue point on the slider to remove the folds in the surface, but that does not change the partial derivatives at the origin. The wrinkle at the origin is enough to make the function non-differentiable.
For the above figures, if you drag the blue dot on the sliders, you can look at other surfaces that are not differentiable. The partial derivatives at the origin do not change, so the candidate for the tangent plane is still the horizontal. However, you can see that the horizontal plane is not a tangent plane.
Note that for these functions, you could write down the matrix of partial derivatives. It would simply be $[0 \, 0]$. But that matrix would not correspond to the derivative.
Further example
The following is another example function that has partial derivatives at the origin but is not differentiable. For this example, we have an equation for the function. \begin{align*} f(x,y) = \begin{cases} \displaystyle \frac{x^2y}{x^2+y^2} & \text{if } (x,y) \ne (0,0)\\ 0 & \text{if } (x,y) = (0.0) \end{cases} \end{align*}
The graph of the function is shown below.
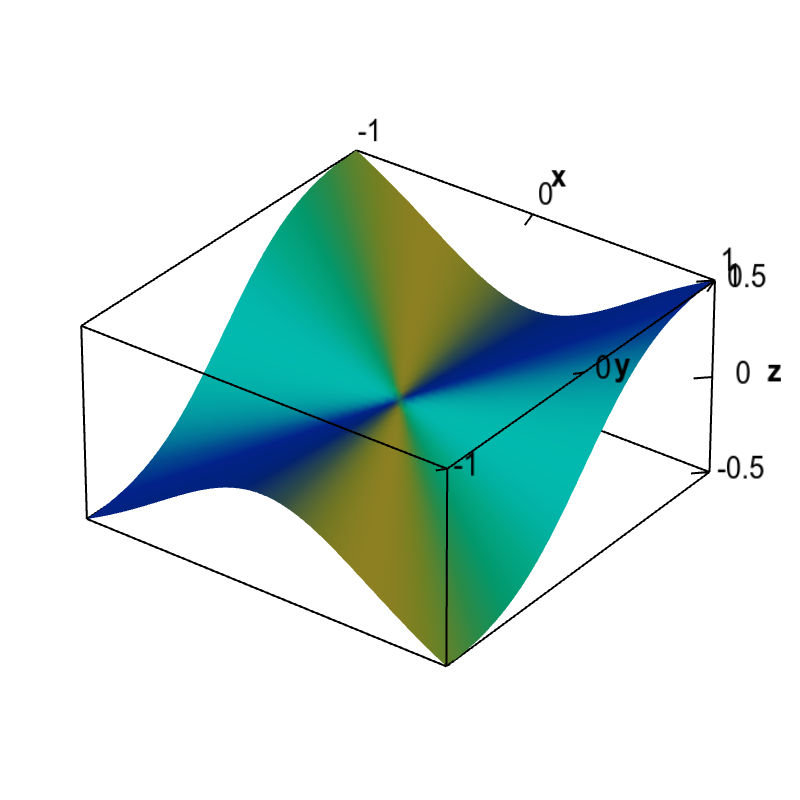
Applet loading
Non-differentiable function with partial derivatives. The partial derivatives of this function $f(x,y)$ are zero at the origin, $\pdiff{f}{x}(0,0)=\pdiff{f}{y}(0,0)=0$. Therefore, the only possibility for a tangent plane would be a horizontal plane. However, since the slopes of this function coming to the origin along different directions are not zero, a horizontal plane cannot be tangent. We conclude that no tangent plane exists at the origin and this function is not differentiable there.
We can show partial derivatives exist at (0,0) but that function is not differentiable at (0,0). Since this function is defined in piecewise fashion around the origin, there are no simple formulas for the partial derivatives. We have to use the limit definition of the partial derivatives. For the partial derivative with respect to $x$, this formula is \begin{align*} \pdiff{f}{x}(0,0) &= \lim_{h \rightarrow 0} \frac{f(0+h,0)-f(0,0)}{h}. \end{align*} Since $f(0,0)=0$ and $f(0+h,0)=f(h,0) = 0$, we calculate \begin{align*} \pdiff{f}{x}(0,0) &= \lim_{h \rightarrow 0} \frac{f(0+h,0)-f(0,0)}{h}\\ &= \lim_{h \rightarrow 0} \frac{0- 0}{h} = \lim_{h \rightarrow 0} 0 =0. \end{align*} Similarly, you can show that $\displaystyle \pdiff{f}{y}(0,0)=0$.
If the function had a tangent plane at (0,0), then it would have to be the flat plane with equation $z=f(0,0)=0$.
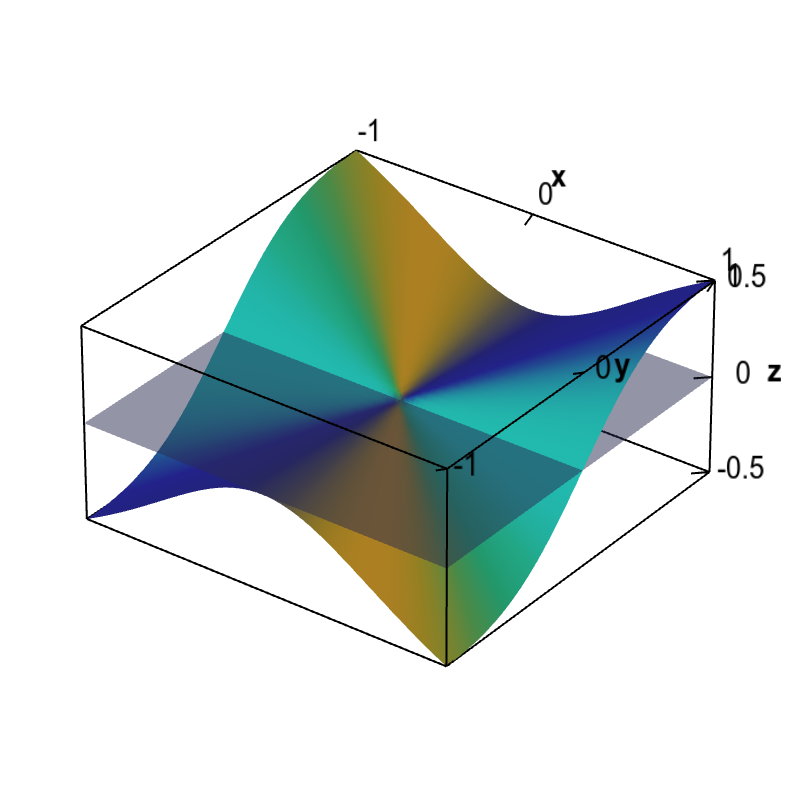
Applet loading
Non-differentiable function with partial derivatives and no tangent plane. A function that is not differentiable at the origin is shown with the only possibility for a tangent plane at the origin. As the partial derivatives are zero at the origin, this candidate plane is a horizontal plane. However, this plane is not tangent since the slopes of this function coming to the origin along different directions are not zero.
As you may see from the graph, if one approaches the origin along a diagonal, the tangent to the path would not be in the plane $z=0$.
Overcoming subtleties
Thankfully, in many cases, there is a simple way to overcome these subtleties and know for sure that a function is differentiable. The differentiability theorem tells us that a function with continuous partial derivatives must be differentiable and therefore cannot have any of the crazy behavior of the above examples. By the same token, since the above functions are not differentiable, they must have discontinuous partial derivatives. For the latter example, we can visualize how it indeed has discontinuous partial derivatives.
Thread navigation
Multivariable calculus
- Previous: The definition of differentiability in higher dimensions
- Next: The multivariable linear approximation
Math 2374
Similar pages
- The derivative matrix
- The definition of differentiability in higher dimensions
- An introduction to the directional derivative and the gradient
- The multidimensional differentiability theorem
- Non-differentiable functions must have discontinuous partial derivatives
- A differentiable function with discontinuous partial derivatives
- Introduction to partial derivatives
- Partial derivative examples
- Partial derivative by limit definition
- Introduction to differentiability in higher dimensions
- More similar pages