Applet: Outward flowing 2D vector field with negative divergence
Applet loading
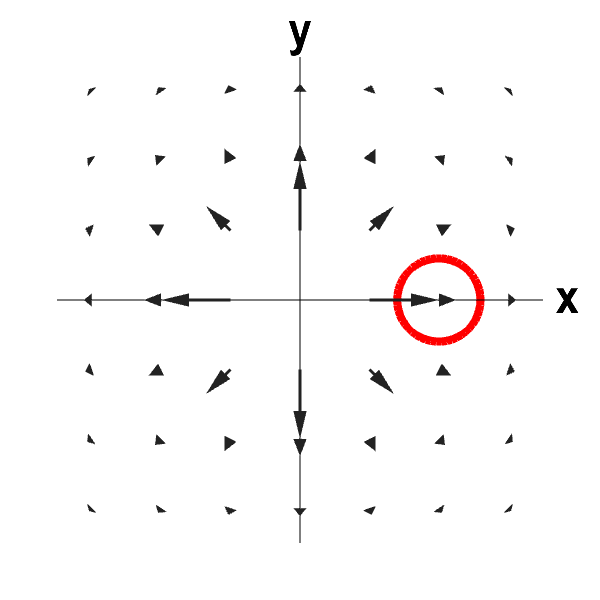
This vector field illustrates some of the subtlety of divergence. The vector field is radiating outward, so it looks like it is expanding. However, the vector field decreases in magnitude with distance from the origin fast enough to outweigh the effect of outward radiation and make the divergence be negative. As long as the circle is away from the origin (the applet ensures this is the case), there is a net flow into the circle. The divergence is not defined at the origin, so we ignore that point.
To reconcile the zero divergence with the picture, notice that, on one hand, the flow out of the circle is slower than the flow into the circle, as the arrows are getting shorter. On the other hand, because the flow is radiating outward, the vector field points into the circle across more than half of its boundary. For this vector field, the first effect wins, and there is a net flow into the circle. If we stay away from the origin, the vector field is compressing and the divergence is zero.
This vector field is $$ \dlvf(x,y) = \frac{(x,y)}{(x^2+y^2)^{3/2}},$$ for $(x,y) \ne (0,0)$. (It is not defined at the origin.) The divergence of $\dlvf$ away from the origin is \begin{align*} \div \dlvf(x,y) &= \pdiff{}{x}\frac{x}{(x^2+y^2)^{3/2}} + \pdiff{}{y}\frac{y}{(x^2+y^2)^{3/2}} \\ &= \frac{(x^2+y^2) - 3x^2} {(x^2+y^2)^{5/2}} + \frac{(x^2+y^2) - 3y^2} {(x^2+y^2)^{5/2}} \\ &= \frac{2(x^2+y^2) - 3(x^2+y^2)} {(x^2+y^2)^{5/2}} = \frac{-1} {(x^2+y^2)^{3/2}} <0 \end{align*}
Applet links
This applet is found in the pages
General information about three.js applets
The applet was made using three.js and requires Javascript as well as a browser that supports WebGL. For most three.js applets, you can drag with the mouse to rotate the view, drag with the right button to pan, and zoom in/out with the mouse wheel. Many applets contain points that you can drag to change values of variables.