Subtleties about divergence
Picture of divergence as expansion
We have shown that the divergence measures expansion or compression of a vector field. We immersed a sphere into a vector field that had positive divergence everywhere, as shown below. No matter where one moves the sphere (using the sliders), more fluid flows out of the sphere than into the sphere, indicating the fluid is expanding.
Applet loading
Divergent vector field with embedded sphere. A sphere is embedded in an expanding vector field that could represent fluid flow. The fact that fluid is flowing out of the sphere is a sign of the positive divergence of the vector field. Rotate with mouse to change perspective.
You can move the sphere by dragging it with the mouse. No matter the sphere's position, more fluid is flowing out of the sphere than into the sphere. This fact suggests that the vector field has positive divergence everywhere.
The vector field pictured is \begin{align*} \dlvf(x,y,z) = (x,y,z). \label{vecfield1} \end{align*} Its divergence is \begin{align*} \div \dlvf(x,y,z) = \pdiff{}{x}x + \pdiff{}{y}y + \pdiff{}{z}z = 1+1+1=3, \end{align*} which is a positive constant independent of the point $(x,y,z)$. The picture of the vector field looks like fluid exploding outward, so it makes sense that the fluid is expanding.
Can a picture be misleading?
As one becomes more sophisticated in mathematical thinking, one discovers that pictures can sometimes be misleading. (One reason mathematicians demand mathematical proof is to ensure they aren't fooling themselves into jumping to conclusions based on incomplete information, such as the information gained solely by exploring pictures.) With regard to divergence, one might wonder if an outward flow, such as pictured above, always means that the divergence of the vector field is positive?
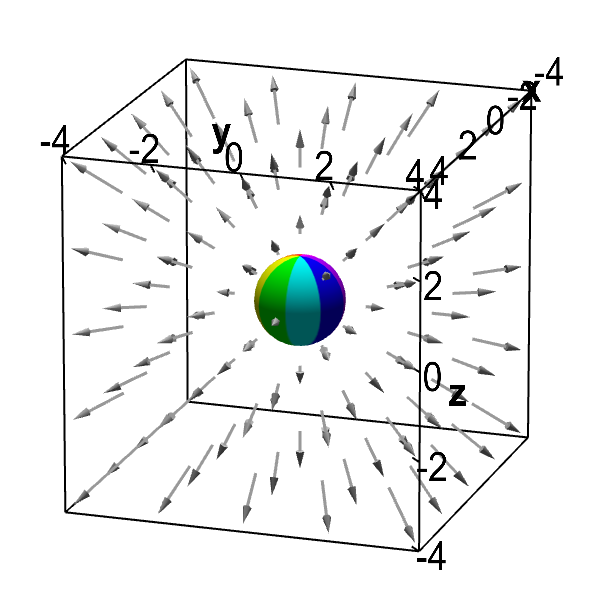
Here's a picture of a different vector field showing fluid flowing outward from the origin. However, it differs from the above vector field in that the arrows get shorter the further they are from the origin. Is the divergence of this vector field positive? In other words, is the fluid expanding as it may look like from the picture?

Applet loading
Outward flowing vector field with zero divergence. This sphere can be moved with the mouse, though it is constrained to stay away from the origin where the vector field isn't defined. Although the vector field is radiating outward, the fluid whose velocity is represented by the vector field is not expanding. As long the the sphere is away from the origin, the same amount of fluid is flowing into as out of the sphere. The divergence of the vector field is zero.
To answer this question, we have to compute the divergence. This vector field is \begin{align*} \dlvf(x,y,z) = \frac{(x,y,z)}{(x^2+y^2+z^2)^{3/2}}, \label{vecfield2} \end{align*} for $(x,y,z) \ne (0,0,0)$. (It is not defined at the origin.) This new vector field is the same as the first vector field above except that we have divided it by its magnitude raised to the third power. (We could write this vector field as $\dlvf(\vc{x}) = \frac{\vc{x}}{\norm{\vc{x}}^3}$, where $\vc{x}=(x,y,z)$.) In this way, the vector field gets smaller as one moves away from the origin.
We calculate the divergence of $\dlvf$: \begin{align*} \div \dlvf(x,y,z) &= \pdiff{}{x}\frac{x}{(x^2+y^2+z^2)^{3/2}} + \pdiff{}{y}\frac{y}{(x^2+y^2+z^2)^{3/2}} + \pdiff{}{z}\frac{z}{(x^2+y^2+z^2)^{3/2}} \\ &= \frac{(x^2+y^2+z^2) - 3x^2} {(x^2+y^2+z^2)^{5/2}} + \frac{(x^2+y^2+z^2) - 3y^2} {(x^2+y^2+z^2)^{5/2}} + \frac{(x^2+y^2+z^2) - 3z^2} {(x^2+y^2+z^2)^{5/2}}\\ &= \frac{3(x^2+y^2+z^2) - 3(x^2+y^2+z^2)} {(x^2+y^2+z^2)^{5/2}} =0 \end{align*}
Hence, as long as we are not at the origin, the divergence is zero and the flow is neither expanding nor contracting.
How can we reconcile this fact with the picture? If the sphere is at the origin, clearly the flow is out of the sphere. But the divergence is not defined at the origin, so we have to ignore that point. If you move the sphere away from the origin, it is not clear if there is more fluid flowing into the sphere or more fluid flowing out. On one hand, the flow out of the sphere is slower than the flow into the sphere, as the arrows are getting shorter. On the other hand, because the flow is radiating outward, the fluid is flowing out of the sphere across more than half of its surface. For this particular vector field, I balanced those two effects (by carefully choosing how quickly the vector field shrinks as one moves away from the origin) so that the net flow into the sphere is exactly equal to the net flow out of the sphere. If we stay away from the origin, the fluid is neither expanding nor compressing and the divergence is zero.
Dependence on dimension
Here's one more subtlety just for fun. To make the divergence zero in the above example, I balanced the outward flow of the vector field by shrinking the vector field as one moves away from the origin. The flow out of the sphere was equal to the flow into the sphere and there was no expansion or compression.
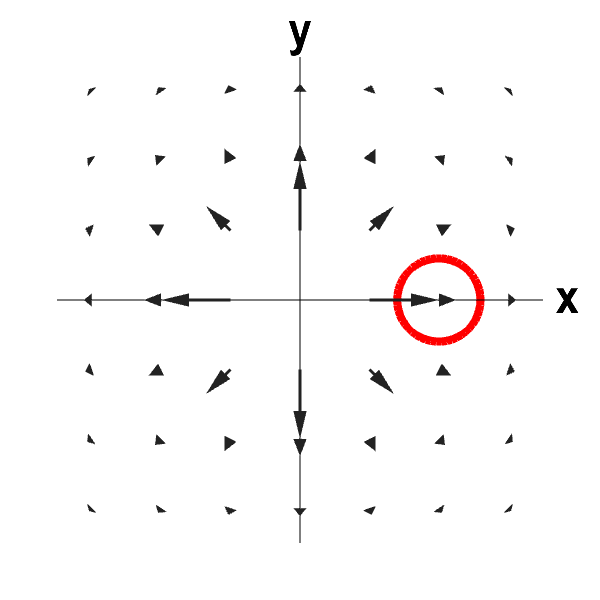
What happens if I take the two-dimensional version of the previous vector field? The 2D vector field is \begin{align*} \dlvf(x,y) = \frac{(x,y)}{(x^2+y^2)^{3/2}}, \end{align*} for $(x,y) \ne (0,0)$. (It is not defined at the origin.) This vector field is shown below along with a circle that you can move by dragging it with your mouse. Given that the circle is away from the origin, is the divergence positive, negative, or zero?
Applet loading
Outward flowing 2D vector field with negative divergence. This circle can be moved by dragging it with the mouse. Although the vector field is radiating outward, it is actually compressing. As long the the circle is away from the origin (where the vector field is not defined), there is a net flux into the circle. The divergence of the vector field is negative.
We calculate the divergence of $\dlvf$: \begin{align*} \div \dlvf(x,y) &= \pdiff{}{x}\frac{x}{(x^2+y^2)^{3/2}} + \pdiff{}{y}\frac{y}{(x^2+y^2)^{3/2}} \\ &= \frac{(x^2+y^2) - 3x^2} {(x^2+y^2)^{5/2}} + \frac{(x^2+y^2) - 3y^2} {(x^2+y^2)^{5/2}} \\ &= \frac{2(x^2+y^2) - 3(x^2+y^2)} {(x^2+y^2)^{5/2}} = \frac{-1} {(x^2+y^2)^{3/2}} <0 \end{align*}
In this case, away from the origin, the divergence is negative. The fluid is compressing even though it is flowing outward.
Why did the dimension make a difference? One can see the difference from the calculations, but what is the difference in the geometric picture? As in the three-dimensional case, the fluid flows into the circle faster than it flows out of the circle, as the arrows are getting shorter. And, as in the three-dimensional case, because the flow is radiating outward, the fluid is flowing out of the circle over more than half the boundary of the circle. But, because we are only in two dimensions, the effect from the boundary is smaller. I chose the vector field to balance the two effects and make the divergence zero in three dimensions. But, this makes the divergence of the two-dimensional analogue be negative.
You can check that the divergence of the vector field \begin{align*} \dlvf(x,y) = \frac{(x,y)}{x^2+y^2} \end{align*} is zero but that the divergence of the three-dimensional analogue \begin{align*} \dlvf(x,y,z) = \frac{(x,y,z)}{x^2+y^2+z^2} \end{align*} is positive. In general, for a number $p$, the divergence of the vector field \begin{align*} \dlvf(\vc{x}) = \frac{\vc{x}}{\norm{\vc{x}}^p} \end{align*} is $\div \dlvf(\vc{x}) = (3-p)/\norm{\vc{x}}^p$ in three dimensions and is $\div \dlvf(\vc{x}) = (2-p)/\norm{\vc{x}}^p$ in two dimensions. So you need $p=3$ to have zero divergence in three dimensions and $p=2$ to have zero divergence in two dimensions.
Thread navigation
Multivariable calculus
Math 2374
- Previous: Divergence and curl example
- Next: Subtleties about curl
Similar pages
- The idea of the divergence of a vector field
- Subtleties about curl
- Divergence and curl notation
- Divergence and curl example
- The idea of the curl of a vector field
- The components of the curl
- Vector field overview
- Vector fields as fluid flow
- A path-dependent vector field with zero curl
- The idea behind the divergence theorem
- More similar pages