Applet: Surface of revolution
Applet loading
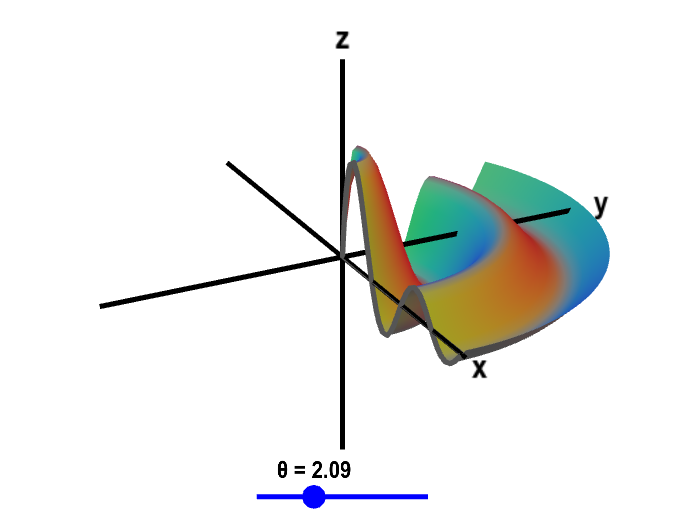
The graph of the function $$f(x,y)=\frac{\sin \sqrt{x^2+y^2}}{\sqrt{x^2+y^2}+1}$$ is a surface of revolution since $f(x,y)$ is a function of just the radius $r=\sqrt{x^2+y^2}$, i.e., $f(x,y)=g\left(\sqrt{x^2+y^2}\right)$ where $g(r)=\sin r/(r+1)$. You can transform between the plot of $g(r)$ and the plot of $f(x,y)$ by changing the rotation angle $\theta$. (Drag the blue point along the slider.) When $\theta=0$, the figure shows the plot of $z=g(x)$ in the $xz$-plane. When $\theta=2\pi$, the figure shows the entire surface of $z=f(x,y)$.
Applet links
This applet is found in the pages
General information about three.js applets
The applet was made using three.js and requires Javascript as well as a browser that supports WebGL. For most three.js applets, you can drag with the mouse to rotate the view, drag with the right button to pan, and zoom in/out with the mouse wheel. Many applets contain points that you can drag to change values of variables.