Surfaces of revolution
Surfaces of revolution are graphs of functions $f(x,y)$ that depend only on the the distance of the point $(x,y)$ to the origin. One way to discuss such surfaces is in terms of polar coordinates $(r,\theta)$.
The coordinate $r$ is the radius from the origin to the point $P$ (or the distance to the origin) and $\theta$ is the angle from the positive $x$-axis. You may recall that we can express the radius $r$ in terms of rectangular (Cartesian) coordinates by $r=\sqrt{x^2+y^2}$. The set of all points where $r$ is constant is a circle of radius $r$ centered around the origin.
Let's say we had a function $f(x,y)$ of a special form so that it depended only on the radius $r$, i.e., depended on $x$ and $y$ only via the expression $\sqrt{x^2+y^2}$. In this case, if we changed $x$ and $y$ in such a way that $r=\sqrt{x^2+y^2}$ didn't change, then the value of the function $f(x,y)$ would not change. Combining this observation with our knowledge about $r$, we conclude that $f(x,y)$ is constant along any circle centered around the origin.
What we've just described is a function of the form $f(x,y)= g\bigl(\sqrt{x^2 + y^2}\bigr)$, where $g(r)$ is some one-variable function. We know, for example, that the function $f(x,y)$ is constant on the circle of radius 2 centered at the origin, because for any point $(x,y)$ where $\sqrt{x^2+y^2}=2$, the value of the function $f(x,y)$ is $g(2)$.
This property makes it simple to graph the surface $z=f(x,y)$ because it follows directly from the graph the curve $z=g(r)$. And you already know how to graph a one-variable function.
To graph $f(x,y)$, we take advantage of the fact that it doesn't change as we rotate around the origin in the $xy$-plane. In three dimensions, the $z$-axis would be pointing out of the screen in the above figure illustrating polar coordinates. Hence, this rotation corresponds to rotation around the $z$-axis. The graph of $f(x,y)$ is the graph of $g(r)$ rotated around the $z$-axis. For this reason, the resulting surface is a called a surface of revolution.
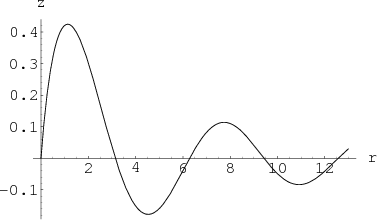
To illustrate, we'll show how the plot of \begin{gather*} z=f(x,y) = \frac{\sin \sqrt{x^2+y^2}} {\sqrt{x^2+y^2}+1} \end{gather*} is a surface of revolution. Since $f(x,y)$ depends on $x$ and $y$ only via the combination $r=\sqrt{x^2+y^2}$, we can rewrite $f(x,y)$ as $f(x,y)= g\bigl(\sqrt{x^2 + y^2}\bigr)$, where \begin{gather*} g(r) =\frac{\sin r} {r+1}. \end{gather*} Here's a plot of $g(r)$.
To help you visualize the relationship between the plot of $g(r)$ and the surface of revolution $z=f(x,y)$, you can transform between the plot of $g(r)$ and the plot of $f(x,y)$ by changing the rotation angle $\theta$ in the following applet.
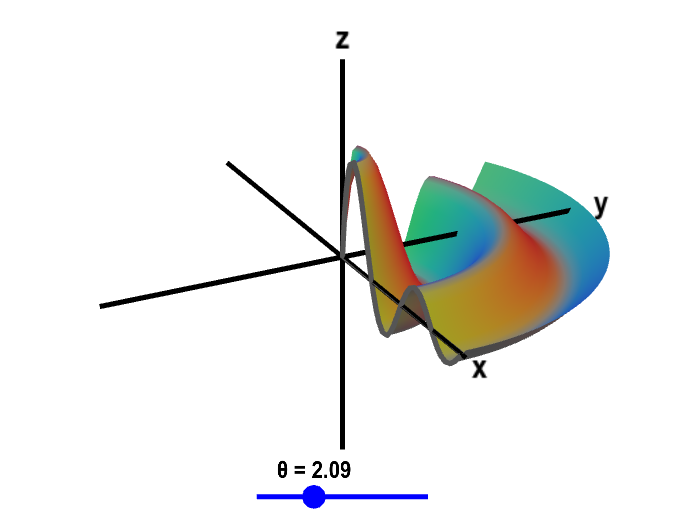
Applet loading
Surface of revolution. The graph of the function $$f(x,y)=\frac{\sin \sqrt{x^2+y^2}}{\sqrt{x^2+y^2}+1}$$ is a surface of revolution since $f(x,y)$ is a function of just the radius $r=\sqrt{x^2+y^2}$, i.e., $f(x,y)=g\left(\sqrt{x^2+y^2}\right)$ where $g(r)=\sin r/(r+1)$. You can transform between the plot of $g(r)$ and the plot of $f(x,y)$ by changing the rotation angle $\theta$. (Drag the blue point along the slider.) When $\theta=0$, the figure shows the plot of $z=g(x)$ in the $xz$-plane. When $\theta=2\pi$, the figure shows the entire surface of $z=f(x,y)$.
Can you recognize that each of these is a surface of revolution?
- $\displaystyle z=\frac{1}{1+x^2+y^2}$
- $z=e^{(x^2+y^2)^3}$
- $z=\sin(\sqrt{x^2+y^2})-x^2-y^2$
Thread navigation
Vector algebra
- Previous: Translation, rescaling, and reflection
- Next: Spherical coordinates