The derivative of the natural logarithm
The derivative of the natural logarithm.
The derivative of the exponential function $f(x)=e^x$ is the function itself: $f'(x)=e^x$. The natural logarithm $\ln(y)$ is the inverse of the exponential function. Can we exploit this fact to determine the derivative of the natural logarithm? Here we present a version of the derivative of an inverse function page that is specialized to the natural logarithm.
To determine how to compute the derivative of the inverse of $f$, let's think about the derivative of $f$ in terms of the function machine metaphor.
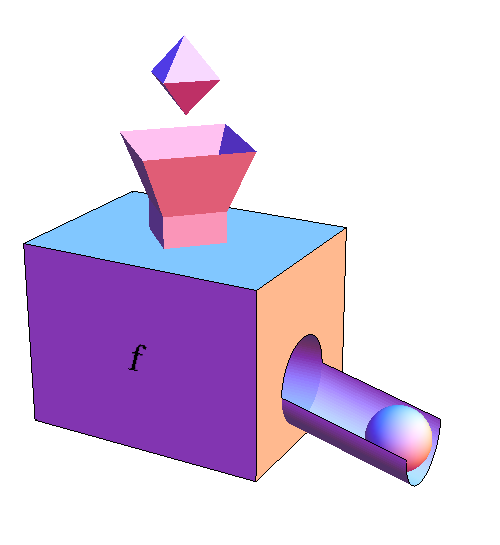
We have denoted the input of $f$ (the tetrahedron) by the variable $x$. Let's denote the output of $f$ (the sphere) by the variable $y$ so that $$y=f(x) = e^x.$$ Since the derivative of $f$ is the ratio of the change in its output to the change in its input, we can write the derivative as \begin{align*} \diff{f}{x}&=\frac{\text{change in output of $f$}}{\text{change in input to $f$}}\\ &= \frac{\text{change in $y$}}{\text{change in $x$}}\\ &=e^x. \end{align*}
Can we do the same thing for the inverse of $f$? Let's use a function machine to represent the inverse of $f$.
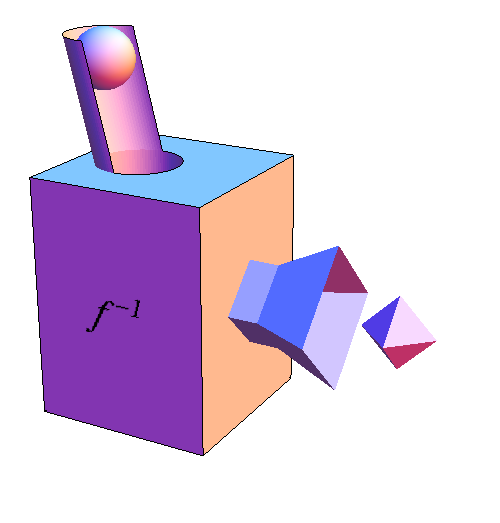
We denote the inverse of $f$ by $f^{-1}$ (pronounced “f inverse”). The input to $f^{-1}$ is the output of $f$ (the sphere), which we have labeled as $y$. The output of $f^{-1}$ is the input to $f$ (the tetrahedron), which we have labeled as $x$. Since the natural logarithm is the inverse of the exponential function, we can write $f^{-1}$ as $$x=f^{-1}(y) = \ln(y).$$
We can represent the derivative of $f^{-1}$ in the same was as we did for $f$. Using that the derivative of $f^{-1}$ is the ratio of the change in its output to the change in its input, we can conclude that \begin{align*} \diff{f^{-1}}{y} &=\frac{\text{change in output of $f^{-1}$}}{\text{change in input to $f^{-1}$}}\\ &=\frac{\text{change in input to $f$}}{\text{change in output of $f$}}\\ &= \frac{\text{change in $x$}}{\text{change in $y$}}. \end{align*} In other words, the derivative of $f^{-1}$ is the reciprocal of the derivative of $f$. Since $f'(x)=e^x$, the derivative of $f^{-1}(y)$ must be $1/e^{x}$. However, since $f^{-1}(y)$ is a function of $y$ (the sphere) not of $x$ (the tetrahedron), we need to rewrite the derivative of $f^{-1}$ in terms of $y$. Since $y=e^{x}$, the derivative of $f^{-1}$ is $1/e^{x}=1/y$, i.e., \begin{align*} \diff{f^{-1}}{y} &= \diff{}{y} \ln(y)\\ &= \frac{1}{y}. \end{align*}
Thread navigation
Math 1241, Fall 2020
Math 201, Spring 22
Similar pages
- The idea of the derivative of a function
- Derivatives of polynomials
- Derivatives of more general power functions
- A refresher on the quotient rule
- A refresher on the product rule
- A refresher on the chain rule
- Related rates
- Intermediate Value Theorem, location of roots
- Newton's Method
- Derivatives of transcendental functions
- More similar pages