Exploring the derivative of the exponential function

The derivative of an exponential function.

The derivative of the exponential function with base 2

In order to take the derivative of the exponential function, say \begin{align*} f(x)=2^x \end{align*} we may be tempted to use the power rule. However, the exponential function $2^x$ is very different from the power $x^2$, because in $2^x$ the variable $x$ itself is in the exponent. We'd get into a lot of trouble with completely bogus results if we replaced the derivative of $2^x$ with $x 2^{x-1}$. Don't do this.

To determine the derivative of the exponential function, we need to go back to the limit definition of the derivative. According to the limit definition, \begin{align} f'(x) &= \lim_{h \to 0}\frac{f(x+h) - f(x)}{h}\notag\\ &= \lim_{h \to 0} \frac{2^{x+h}-2^x}{h}. \label{limit_definition_2_to_x} \end{align} Here we used $h$ for the step size instead of $\Delta x$, but it doesn't matter what we call it.

The situation might look hopeless, until we remember the rules for exponents. We can replace $2^{x+h}$ with $2^x 2^h$ in the numerator. Then, we can factor $2^{x}$ out of the numerator since $2^{x}2^h-2^x = 2^x(2^h-1)$. In fact, we can do even better than that. The factor $2^x$ doesn't even depend on $h$, so we are allowed to pull it out of the limit. Our resulting simplified form for the derivative of $2^x$ is \begin{align} f'(x) &= 2^x \lim_{h \to 0} \frac{2^{h}-1}{h}. \label{limit_number} \end{align}

Did we make any progress? We calculated that the derivative of the function $f(x)=2^x$ is equal to the function itself ($2^x$) times a mysterious looking expression involving a limit. But, the mysterious expression involving a limit is just a single number. Nothing more, nothing less. What number is it? It's an irrational number, but you can estimate it yourself by calculating $(2^h-1)/h$ for smaller and smaller values of $h$.

Use the following applet to estimate $$\lim_{h \to 0} \frac{2^{h}-1}{h}.$$ Type in smaller and smaller values of $h$ in the first column, and it will display $(2^h-1)/h$ in the second column, calculated using the values of $h$ you entered. When you keep making $h$ smaller and smaller, you'll notice that eventually, the first four digits of $(2^h-1)/h$ don't change any more. Those four unchanging digits are an estimate of the number $$\lim_{h \to 0} \frac{2^{h}-1}{h}$$ accurate to four decimal places. Since $h$ can be positive or negative, also check negative values of $h$ to make sure that $(2^h-1)/h$ approaches the same number as $h$ approaches zero from below.

Limit of b to the h minus one over h as h tends to zero. To estimate the limit $\lim_{h \to 0} (b^h-1)/h,$ one can calculate $(b^h-1)/h$ for smaller and smaller values of $h$. The value of $b$ is determined by the number in the third column, which defaults to $b=2$. Enter a value for $h$ in the first column; the corresponding value of $(b^h-1)/h$ is displayed in the second column. To estimate the limit, enter smaller and smaller value of $h$. You should notice that, for sufficiently small values of $h$, the first few digits of $(b^h-1)/h$ remain unchanged as you make $h$ even smaller. In that case, those unchanged digits represent a good estimate of the limit, accurate to the number of digits than remain unchanged. One should obtain the same limiting value if one uses negative values for $h$ and enters successive values of $h$ that are smaller and smaller in absolute value (i.e., closer to zero).

More information about applet.

However, we can do even better than this. Look at the limit definition of equation \eqref{limit_definition_2_to_x} for $f'(x)$, and plug in $x=0$. What do you get? You get exactly \begin{align} f'(0) = \lim_{h \to 0} \frac{2^{h}-1}{h}. \end{align} Our mysterious number in equation \eqref{limit_number} for the derivative $f'(x)$ is just the derivative itself evaluated at $x=0$. We can rewrite expression \eqref{limit_number} for the derivative of $f(x)=2^x$ as \begin{align} f'(x) &=f(x) f'(0). \label{derivative_f_fprime} \end{align}

Equation \eqref{derivative_f_fprime} states that the derivative $f'(x)$ is just equal to the function $f(x)$ itself, multiplied by our mysterious number, which is also the slope $f'(0)$ of the tangent line at $x=0$. This is a strange conclusion, so we better confirm that it is really true.

Use the following applet to convince yourself that the result is valid. Check that the derivative $f'(x)$ is really a multiple of the function $f(x)$ by verifying that the ratio $f'(x)/f(x)$ doesn't change as you change $x$. This ratio should be $f'(0)$, which should be the mysterious number you estimated to four digits as well as the slope of the tangent line when $x=0$.

The derivative of an exponential function. Illustration of how the derivative of the exponential function is a multiple of the function, where that multiple is the derivative at zero. The graph of the function $f(x)=b^x$, where you can enter a value for $b$, is shown by the thick blue curve. The graph of its derivative $f'(x)$ is shown by the thin green curve, and the ratio $f'(x)/f(x)$ is shown by the horizontal gray line. The value of the function and its derivative evaluated at $x_0$ are displayed at the left and illustrated by the blue and green points on the curves. You can change $x_0$ by typing in a new value or dragging one of the points. The red line is the tangent line at $x_0$ with slope $f'(x_0)$. The ratio $f'/f$ evaluate at $x_0$ is also displayed at the left. If you check the “more options” check box, the function changes to $f(x)=c b^{kx}$ and two new boxes appear in which you can change the values of $c$ and $k$. You can use the buttons at the top to zoom in and out as well as pan the view.

More information about applet.

Assuming you've verified that equation \eqref{derivative_f_fprime} seems to be correct, we've done all we can for the derivative of $f(x)=2^x$. The result is just expressed in terms of the mysterious number $$f'(0) = \lim_{h \to 0} \frac{2^h-1}{h},$$ but it is just some irrational number which you've estimated.

Exponential functions with other bases

Does the result that we obtained for $f(x)=2^x$ generalize to other bases besides base 2? See if you can get similar results for the exponential function $$g(x)=b^x$$ where the base $b$ is a positive parameter.

First, repeat the same analytic calculation, starting with the limit definition and replacing 2 with $b$. You should obtain that \begin{align*} g'(x) &=g(x) g'(0) \end{align*} where \begin{align*} g'(0) = \lim_{h \to 0} \frac{b^h-1}{h}. \end{align*}

Second, pick two other values of $b$ besides $b=2$. Try one value of $b$ less than one and one value of $b$ greater than one, so you experiment with both exponential decay and exponential growth. For each of your choices for $b$, use the first applet to estimate the first four digits of the value of the mysterious limit expression defining $g'(0)$. Then, use the second applet to verify that this value is both the derivative $g'(0)$ at zero and the ratio between the derivative $g'(x)$ and the function $g(x)$.

The exponential function with base $e$

As you should have experienced, the mysterious limit expression $$\lim_{h \to 0} \frac{b^h-1}{h}$$ is pretty annoying. Sure it is just a number, but it's some crazy irrational number that is different for each value of the base $b$. Everytime you'd like to calculate the derivative of $b^x$ for another base $b$, you'd have to go through the same calculation to determine the mysterious factor. That's inconvenient, and, moreover, you'd have to come up with some nice way to communicate your result to others.

Let's take a slightly different approach. We'll use the fact that $$\lim_{h \to 0} \frac{b^h-1}{h}$$ changes with the base $b$ to our advantage. Let's find a value of $b$ for which the mysterious factor is as simple as possible: the value 1. Using either the first applet with a very small $h$ or the second applet, experiment with different values of $b$ to find a particular value of $b$ where $$\lim_{h \to 0} \frac{b^h-1}{h} \approx 1.$$

Were you able to find such a number? It turns out there is only one value of $b$ for which the mysterious factor is exactly one. We denote this number by $e$, which is defined to be the one number for which $$\lim_{h \to 0} \frac{e^h-1}{h} = 1.$$ Since $e$ is irrational, we won't be able to get an exact representation of this number using these methods. But, if you were really patient and had a tool like these applets that could estimate the limit with sufficient accuracy, you could estimate $e$ to 30 digits, and determine that $$e \approx 2.71828182845904523536028747135.$$ The above applets understand $e$, so you can type in $e$ for $b$ in either applet and see that the mysterious limit is indeed one for this case.

Another way to see this is to plot the mysterious limit as a function of $b$ and to observe that it crosses one when $b=e$.

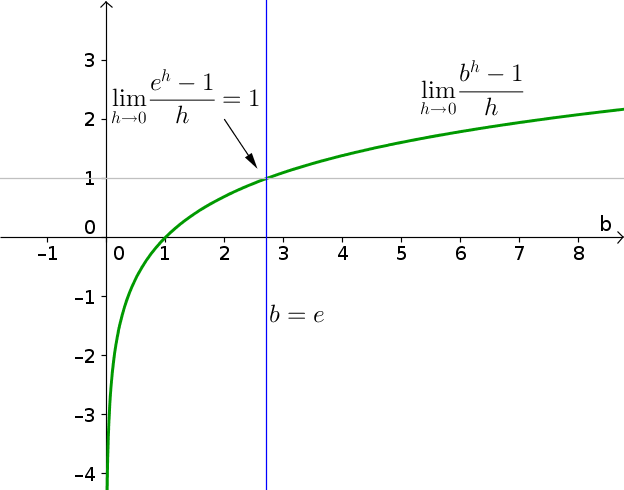
The limit of e to the h minus 1 over h is equal to one

We can conclude that for $b=e$, the derivative of the function $$g(x)=e^x,$$ evaluated at zero is $g'(0)=1$. This means that the derivative of $g$ is exactly the function itself: \begin{align*} g'(x)=g(x). \end{align*} For this reason, only when you enter $e$ for $b$ in the second applet do the function and its derivative exactly coincide.

This fundamental property of $e^x$, that it is its own derivative, is one of the reasons that $e$ is the most common base used for the exponential function throughout the sciences. The function $e^x$ is often referred to as simply the exponential function.

Adding parameters to the exponential function

When discussing the exponential function, we introduced a few parameters, writing the general exponential function as $$f(x)=cb^{kx}$$ with parameters $b$, $c$, and $k$. We then showed how the parameters $b$ and $k$ were redundant, so we only needed one of them. Since we found $b=e$ makes the derivatives nice, let's just use the base $e$ and write our exponential functions as $$f(x)=ce^{kx},$$ which has just two parameters $c$ and $k$.

Do the parameters $c$ and $k$ change the properties of the exponential function? So far, we've just looked at the case where $c=1$ and $k=1$ and found that $f'(x)=f(x)$. Is $f'(x)=f(x)$ for other values of $c$ and $k$? You can use the second applet, above, to explore this question. Check the “more options” check box, which will reveal boxes in which to change $c$ and $k$. You can observe if the graph of $f$ and $f'$ are still identical and if the ratio $f'/f$ is still one when $b=e$ but $c$ and $k$ are different values. If the ratio $f'(x_0)/f(x_0)$ changes when you change $c$ or $k$, is the value still independent of $x_0$? (In other words, is $f'$ still a multiple of $f$?) How does the ratio depend on $c$ and $k$?

To obtain a definitive answer on the derivative of $f(x)=ce^{kx}$, we can repeat the above calculation using the limit definition. \begin{align*} f'(x_0) &= \lim_{h \to 0} \frac{f(x_0+h) - f(x_0)}{h}\\ &= \lim_{h \to 0} \frac{ce^{k(x_0+h)}-ce^{kx_0}}{h} \end{align*} Again, the rules for exponents help us simplify this limit. Since $e^{k(x_0+h)} = e^{kx_0+kh} = e^{kx}e^{kh}$, we can factor out a $ce^{kx_0}$ from the numerator: $ce^{kx_0}e^{kh}-ce^{kx_0} = ce^{kx_0}(e^{kh} -1)$. The number $ce^{kx_0}$ is the same thing as $f(x_0)$. It doesn't depend on $h$, so we can pull it out of the limit and conclude that \begin{align*} f'(x_0) &= f(x_0) \lim_{h \to 0} \frac{e^{kh}-1}{h}. \end{align*}

Except for the factor of $k$ in the exponent, we have exactly the same expression as before. The parameter $c$ doesn't change the result (as presumably you determined from exploring the applet). The parameter $k$ does change things, though, as it alters the mysterious limit expression. Can we reduce this new mysterious limit back into the old one?

We can get our old mysterious limit back with just one manipulation. Let's define a new quantity to be equal to the exponent in our new expression: $w = kh$. Since $h=w/k$, we can rewrite the fraction inside the limit as $$\frac{e^{w}-1}{w/k} = k\frac{e^{w}-1}{w}.$$ Since the parameter $k$ is just some number, the new quantity $w=kh$ goes to zero just as $h$ is going to zero. So, we can replace the limit $h \to 0$ with the equivalent limit $w \to 0$. We can rewrite the new mysterious limit as \begin{align*} \lim_{h \to 0} \frac{e^{kh}-1}{h} &= k \lim_{w \to 0} \frac{e^{w}-1}{w}. \end{align*}

But wait, the $w$ limit is exactly the same as our original myterious limit. OK, it is written in terms of $w$ rather than the original $h$. But that is just notation; it doesn't matter what symbol we use for the quantity that goes to zero in the limit. All the following expressions are exactly the same number. \begin{align*} \lim_{h \to 0} \frac{e^h-1}{h} &= \lim_{w \to 0} \frac{e^{w}-1}{w}\\ &=\lim_{\bigstar \to 0} \frac{e^\bigstar-1}{\bigstar} \end{align*} And what number are these expressions equal to again? Remember the definition of the number $e$. It is exactly the number that makes these limits equal to 1.

Therefore \begin{align*} \lim_{h \to 0} \frac{e^{kh}-1}{h} &= k \lim_{w \to 0} \frac{e^{w}-1}{w} = k \cdot 1 = k, \end{align*} and the derivative of $f(x)=ce^{kx}$ is \begin{align*} f'(x_0) &= f(x_0) \lim_{h \to 0} \frac{e^{kh}-1}{h} = kf(x_0). \end{align*} It's that simple, and you probably figured this out already from exploring the applet. When you differentiate $e^{kx}$, you just get the function back again, multiplied by the parameter $k$.

Let's write this result using some fancy notation. Recall that we can write the derivative $f'(x)$ also as $\diff{f}{x}(x)$. We can separate this into $\diff{}{x} f(x)$. The $\diff{}{x}$ by itself means to take the derivative of whatever comes after it, where $x$ is the variable. (We often say “taking the derivative with respect to $x$.”) Using this $\diff{}{x}$ notation, we can write our result for the derivative of $e^{kx}$ as \begin{align} \diff{}{x} e^{kx} = ke^{kx}. \label{derivative_ekx}\tag{5} \end{align}

What is this mysterious limit?

We have just one more matter of business before we've wrapped up our exploration of the derivative of the exponential function. What about the derivative of exponential functions with base $b$ equal to a number besides $e$? According to our calculations, the derivative of $g(x)=b^x$ is equal to $g'(x) =g(x) g'(0)$, where the factor $g'(0)$ was the mysterious limit \begin{align*} g'(0) = \lim_{h \to 0} \frac{b^h-1}{h}. \end{align*} Let's see if we can find a nicer looking expression for that limit. It will still probably be some irrational number, but we'll look for a better way to calculate this expression than trying to evaluate the limit directly.

The answer is one simple trick. We can turn any exponential base $b$ into the nicer exponential base $e$. We just have to remember that the inverse of the exponential function $e^x$ is the logarithm base $e$, or the natural logarithm. We often write the natural logarithm of $x$ simply as $\log x$, because if you are going to take a logarithm and no one tells you otherwise, you might as well do the natural thing and use base $e$. To be absolutely explicit, we can also use the notation $\ln x$ for the natural logarithm, which we'll use for now.

Since $\ln x$ and $e^x$ are inverses, it follows that for any number $x>0$, we can also write $x$ as $$x = e^{\ln x}.$$ If instead of $x$, we insert the expression $b^x$, we can rewrite $b^x$ as $$b^x = e^{\ln b^x} = e^{x \ln b},$$ where for the last step, we used one of the basic rules for logarithms: $\log b^x = x \log b$. We've determined that $b^x$ is the same thing as $e^{kx}$ where $k=\ln b$. This explains why $k$ and $b$ are redundant parameters of the exponential function. We don't need to use $b^x$ with different bases $b$, we could get the same function by using $e$ for the base and writing the function as $e^{kx}$ where $k=\ln b$.

Given that $k=\ln b$, we can use formula \eqref{derivative_ekx} for the derivative of $e^{kx}$ to compute the derivative of $b^x$. We just need to multiply the function by $k$, which is the same thing as multiply by $\ln b$. Our revised formula for the derivative of $b^x$ is \begin{align*} \diff{}{x} b^x = b^x \ln b. \end{align*}

Finally we've figured out what the mysterious limit was. The mysterious limit was simply $\ln b$ in disguise: \begin{align*} \lim_{h \to 0} \frac{b^h -1}{h} = \ln b. \end{align*}

In case you aren't comfortable with these manipulations, you should do the best to convince yourself that this limit is the natural logarithm. Test it out on a calculator. When you enter $\ln 2$, do you get a result similar to the estimate you made above for the limit $\lim_{h \to 0} (2^h-1)/h$? Look at how the graph of $(b^h-1)/h$ for different values of $h$ converges $\ln b$ as $h$ gets smaller and smaller.

Limit of b to the h minus one over h as h tends to zero converges to the natural logarithm. Demonstration that a function $m(b)=(b^h-1)/h$ approaches the natural logarithm in the limit that the parameter h goes to zero. For a given value of $h$, determined by the red slider, $(b^h-1)/h$ is plotted as a function of $b$ by the thin green curve. The graph of the function $\ln b$ is plotted by the thick blue curve. As you change $h$ to make it closer and closer to zero, the thin green curve converges to the thick blue curve, demonstrating that $(b^h-1)/h$ approaches $\ln b$ as $h$ approaches zero.

More information about applet.

It's a lot nicer to have a formula for the derivative of $b^x$ without the mysterious limit, using $\ln b$ instead. Usually, in calculus, though, we'll stay away from bases another than the natural one $e$. The most important of the formulas that we've derived are $$\diff{}{x}e^x = e^x$$ and its generalization $$\diff{}{x}e^{kx} = ke^{kx}.$$ (You can always multiply either formula by a constant number $c$.)

In fact, $e^{x}$ (including its multiples $ce^{x}$) is the only function that is its own derivative. So, if you were told to find a function $f(x)$ where $f'(x)=f(x)$, you'd know that the function must be $f(x)=ce^x$ for some (unknown) number $c$.

The worksheet on exploring the derivative of the exponential function contains questions to guide you through discovering the properties of the exponential function derivative.

Math Insight