Image: Double integral as volume under a surface, with box illustrating Riemann sum
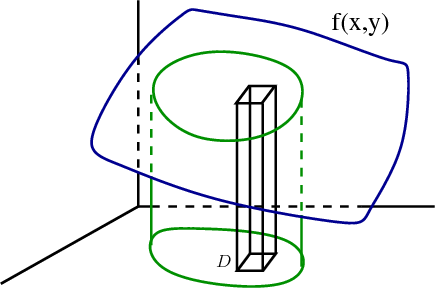The double integral $\iint_{\dlr} f(x,y) dx\,dy$ for $f(x,y)>0$ can be interpreted as the volume under the surface $z =f(x,y)$ over the region $(x,y) \in \dlr$. This volume can be estimated by a Riemann sum, where each term corresponds to the volume of a little box.
Image file: double_integral_volume_under_surface_box.png
Image links
This image is found in the pages