Image: The line integral of a conservative vector field
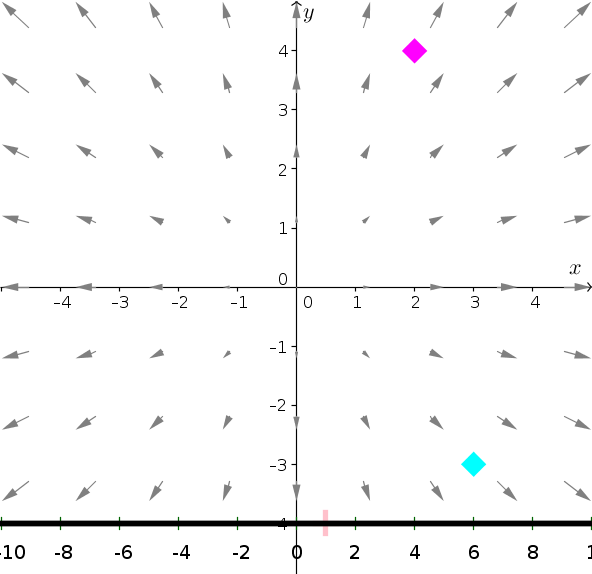
Since the vector field $\dlvf(x,y)=(x,y)$ is conservative, the line integral of $\dlvf$ from the point $\vc{a}=(3,-3)$ to the point $\vc{b}=(2,4)$ is 1 (shown by magenta line on slider), independent of the path from $\vc{a}$ to $\vc{b}$.
A potential function of $\dlvf(x,y)$ is $f(x,y)=\frac{1}{2}x^2 + \frac{1}{2}y^2$, as $\nabla f = \dlvf$. Therefore, by the gradient theorem, the integral is $f(\vc{b})-f(\vc{a}) = 10-9=1$.
Image file: line_integral_conservative_vector_field.png
Source image file: line_integral_conservative_vector_field.ggb
Source image type: Geogebra
Image links
This image is found in the pages