An introduction to conservative vector fields
Many physical force fields (vector fields) that you are familiar with are conservative vector fields. The term comes from the fact that some kind of energy is conserved by these force fields. The important consequence for us, though, is that as you move an object from point $\vc{a}$ to point $\vc{b}$, the work performed by a conservative force field does not depend on the path taken from point $\vc{a}$ to point $\vc{b}$. For this reason, we often refer to such vector fields as path-independent vector fields. Path-independent and conservative are just two terms that mean the same thing.
For example, imagine you have to carry a heavy box from your front door to your bedroom upstairs. Because of the gravity (which can be viewed as a force field), you have to do work to carry the box up.
Here we mean the scientific definition of work, which is force times distance. Although it may feel like work to move the box from one room to another on the same floor, the actual work done against gravity is zero.
Next, imagine that you have two stairways in your house: a gently sloping front staircase, and a steep back staircase. Since the gravitational field is a conservative vector field, the work you must do against gravity is exactly the same if you take the front or the back staircase. As long as the box starts in the same position and ends in the same position, the total work is the same. (In fact, if you decided to first carry the box to your neighbor's house, then carry it up and down your backyard tree, and then in your back door before taking it upstairs, it wouldn't make a difference for this scientific definition of work. The net work you performed against gravity would be the same.)
The line integral of a vector field can be viewed as the total work performed by the force field on an object moving along the path. For the above gravity example, we discussed the work you performed against the gravity field, which is exactly opposite the work performed by the gravity field. We'd need to multiply the line integral by $-1$ to get the work you performed against the gravity field, but that's a technical point we don't need to worry much about.
The above discussion implies that if $\dlvf$ is a conservative vector field, then the integral \begin{align*} \dlint \end{align*} does not actually depend on the path $\dlc$. It only depends on the beginning point (say $\vc{a}$) and endpoint (say $\vc{b}$) of the path $\dlc$. If we changed the path $\dlc$ to a different path $\adlc$, then we know that \begin{align*} \dlint = \lint{\adlc}{\dlvf} \end{align*} as long as the path $\adlc$ also starts at the point $\vc{a}$ and ends at the point $\vc{b}$. This property is certainly not true for all vector fields $\dlvf$ (as shown below). It is only true for the special class of conservative vector fields, which is why we can call them path-independent vector fields.
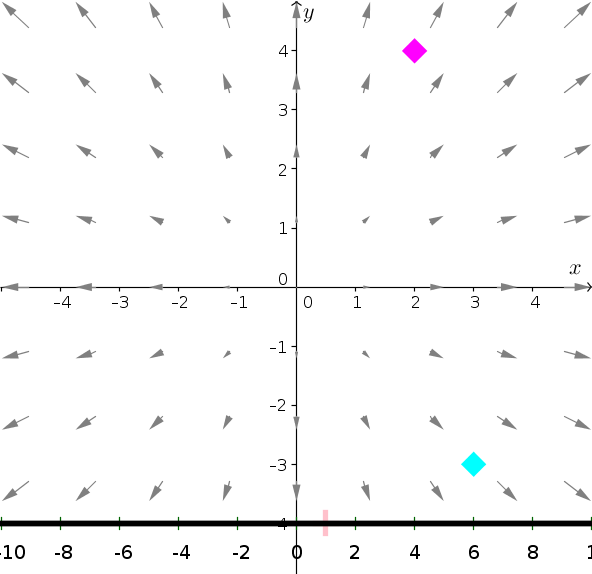
The vector field $\dlvf(x,y)=(x,y)$ is a conservative vector field. (You can read how to test for path-independence later. For now, take it on faith.) It is illustrated by the black arrows in the below figure. We want to compute the integral \begin{align*} \dlint \end{align*} where $\dlc$ is a path from the point $\vc{a}=(3,-3)$ (shown by the cyan square) to the point $\vc{b}=(2,4)$ (shown by the magenta square). Since $\dlvf$ is path-independent, we don't need to know anything else about the path $\dlc$ to compute the line integral. Later, you'll learn to compute that the value of the integral is 1, as shown by the magenta line on the slider below the figure.
The below applet demonstrate the path-independence of $\dlvf$, as one can see that the integrals along three different paths give the same value. The vector field appears to be path-independent, as promised. (You'd have to check all the infinite number of possible paths from all points $\vc{a}$ to all points $\vc{b}$ to determine that $\dlvf$ was really path-independent. Fortunately, you'll learn some simpler methods.)
The line integral over multiple paths of a conservative vector field. The integral of conservative vector field $\dlvf(x,y)=(x,y)$ from $\vc{a}=(3,-3)$ (cyan diamond) to $\vc{b}=(2,4)$ (magenta diamond) doesn't depend on the path. Path $\dlc$ (shown in blue) is a straight line path from $\vc{a}$ to $\vc{b}$. Paths $\adlc$ (in green) and $\sadlc$ (in red) are curvy paths, but they still start at $\vc{a}$ and end at $\vc{b}$. Each path has a colored point on it that you can drag along the path. The corresponding colored lines on the slider indicate the line integral along each curve, starting at the point $\vc{a}$ and ending at the movable point (the integrals alone the highlighted portion of each curve). Moving each point up to $\vc{b}$ gives the total integral along the path, so the corresponding colored line on the slider reaches 1 (the magenta line on the slider). This demonstrates that the integral is 1 independent of the path.
Of course, the line integrals to intermediate points can vary widely. By comparing the tangent vectors of the curves to the vector field, you should be able to explain the behavior of the line integrals to intermediate points. In particular, you can determine why the line integral increases or decreases by comparing the direction of motion along the path to the direction of the vector field.
A path-dependent vector field
As mentioned above, not all vector fields are conservative. If a vector field is not path-independent, we call it path-dependent (or non-conservative). The vector field $\dlvf(x,y) = (y, -x)$ is an example of a path-dependent vector field. This vector field represents clockwise circulation around the origin. It turns out, such circulation is the key indicator of path-dependence (however, the circulation may not be as obvious as it is in this example). Again, you can read the details later.
For a path-dependent vector field, the line integral from $\vc{a}$ to $\vc{b}$ isn't defined until you specify a path, as the value can depend on the details of the path. The vector field $\dlvf(x,y) = (y, -x)$ and three paths from $\vc{a}=(0,-4)$ to $\vc{b}=(0,4)$ are shown in the below applet. The three paths demonstrate that $\dlvf$ is indeed path-dependent, as the three integrals from $\vc{a}$ to $\vc{b}$ have different values. Indeed, you only need to show that the integrals along two paths from some point $\vc{a}$ to some other point $\vc{b}$ are not the same in order to prove that $\dlvf$ was path-dependent (since if $\dlvf$ were path-independent, this could never happen).
The line integral of a path-dependent vector field. The vector field $\dlvf(x,y) = (y,-x)$ and three paths from $\vc{a}=(0,-4)$ (the cyan diamond) to $\vc{b}=(0,4)$ (the magenta diamond) as shown. Path $\dlc$ (shown in blue) is a straight line path from $\vc{a}$ to $\vc{b}$. Paths $\adlc$ (in green) and $\sadlc$ (in red) are clockwise and counterclockwise, respectively, circular path from $\vc{a}$ and to $\vc{b}$. You can drag the colored points, and the corresponding color lines on the slider indicate the line integral of $\dlvf$ from $\vc{a}$ along the path up to the colored point (the highlighted portion of the curve). Even when you drag the points to $\vc{b}$, the values of the line integrals have different values, demonstrating that $\dlvf$ is indeed path-dependent.
Path $\dlc$ (in blue) is a straight line up the $y$-axis. Along the $y$-axis, $\dlvf(0,y)=(y,0)$ is horizontal. Hence the direction of motion and the vector field are orthogonal, and \begin{align*} \dlint =0. \end{align*} On the other hand, path $\adlc$ (in green) goes with the clockwise rotation of the vector field. Consequently, the work performed by the vector field is positive, and \begin{align*} \lint{\adlc}{\dlvf} >0. \end{align*} The same reasoning shows that \begin{align*} \lint{\sadlc}{\dlvf} <0, \end{align*} since the counterclockwise direction of path $\sadlc$ (in red) is opposite the direction of the vector field. Since all three paths start at $\vc{a}$ and end at $\vc{b}$, these results confirm that $\dlvf$ is path-dependent.
Calculating integrals of conservative vector fields
One of the four fundamental theorems of vector calculus is the gradient theorem for line integrals, which gives a nice way to calculate of line integral of conservative vector fields. To use the gradient theorem, one needs to determine if a vector field is conservative. If a vector field is conservative, one can find a potential function analogous to the potential energy associated with conservative physical forces. Once the potential function is known, it is very simple to calculate line integrals, as shown by this example of calculating a line integral using the gradient theorem.
Thread navigation
Multivariable calculus
Math 2374
Notation systems
Similar pages
- How to determine if a vector field is conservative
- The gradient theorem for line integrals
- A path-dependent vector field with zero curl
- A conservative vector field has no circulation
- Finding a potential function for conservative vector fields
- Finding a potential function for three-dimensional conservative vector fields
- A simple example of using the gradient theorem
- Testing if three-dimensional vector fields are conservative
- Vector field overview
- Vector fields as fluid flow
- More similar pages