Image: A stretching two-dimensional linear transformation
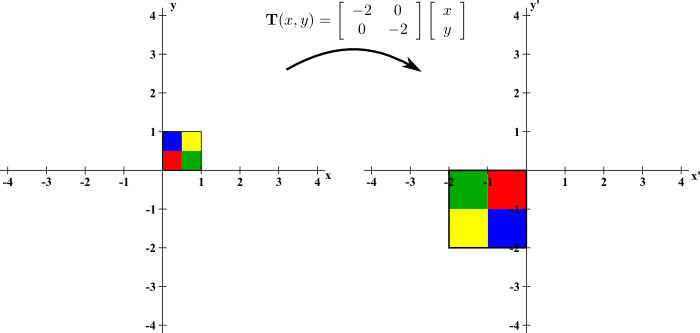The linear transformation $$\vc{T}(x,y) = \left[\begin{array}{cc}-2 &0\\ 0 &-2\end{array}\right]\left[\begin{array}{c}x\\y\end{array}\right]$$ rotates objects by $\pi$ radians and stretches to increase area by a factor of 4. It maps the unit square $[0,1]\times[0,1]$ into a $2 \times 2$ square of area 4. Although it rotates, it preserves orientation, as illustrated by the same ordering of colors as one moves counterclockwise around the perimeter of both squares. These properties are reflected by the fact that the determinant of the associated matrix is 4.
Image file: linear_transformation_2d_m2_0_0_m2.png
Source image file: linear_transformation_2d_m2_0_0_m2.svg
Source image type: Inkscape SVG
Image links
This image is found in the pages