Determinants and linear transformations
A linear transformation $\vc{T}: \R^n \to \R^m$ (confused?) is a mapping from $n$-dimensional space to $m$-dimensional space. Such a linear transformation can be associated with an $m \times n$ matrix.
If we restrict ourselves to mappings within the same space, such as $\vc{T}: \R^n \to \R^n$, then $\vc{T}$ is associated with a square $n \times n$ matrix. One can calculate the determinant of such a square matrix, and such determinants are related to area or volume. It turns out that the determinant of a matrix tells us important geometrical properties of its associated linear transformation. We'll outline this relationship for one-dimensional, two-dimensional, and three-dimensionional linear transformations.
One-dimensional linear transformations
A one-dimensional linear transformation is a function $T(x) = ax$ for some scalar $a$. To view the one-dimensional case in the same way we view higher dimensional linear transformations, we can view $a$ as a $1 \times 1$ matrix. The determinant of the $1 \times 1$ matrix is just the number $a$ itself. Although this case is very simple, we can gather some intuition about linear maps by first looking at this case.
An example one-dimensional linear transformation is the function $T(x)=3x$. We could visualize this function by its graph, which is a line through the origin with slope 3. However, instead, let's view it as a mapping from the real line $\R$ back onto the real line $\R$. In this case, we think of the function as $x' = T(x)$, which maps the number $x$ on the $x$-axis to the new number $T(x)$ on an $x'$-axis. $T$ takes the number 1 and maps it to 3. $T$ maps 0 to 0 and -1/2 to -3/2. We also use the language that 3 is the image of 1 under the mapping $T$.
We can summarize this mapping by looking how $T$ maps an interval of numbers. For example, $T$ maps the interval $[0,1]$ to the interval $[0,3]$, as illustrated by the following figure. We colored the interval $[0,1]$ and its image $[0,3]$ with a green to red gradient that illustrates how each point in the interval is mapped by $T$. A point of a given color in $[0,1]$ is mapped to a point of the same color in the image $[0,3]$.
The fact that the determinant of the matrix associated with $T$ is 3 means that $T$ stretches objects so that their length is increased by a factor of 3. Since the determinant was positive, $T$ preserves the orientation of objects: in both the interval $[0,1]$ and its image $[0,3]$, red points are to the right of green points.
Another examples is the linear transformation $T(x)=-\frac{1}{2}x$. As shown in the below figure, $T$ maps the interval $[0,1]$ onto the interval $[-\frac{1}{2},0]$. The determinant of the matrix associated with $T$ is $-\frac{1}{2}$. Since the magnitude of this determinant is $\frac{1}{2}$, $T$ shrinks objects to be half their original length. The negative determinant indicates that $T$ reverses the orientation of objects: as indicated by the colors, the right of the interval $[0,1]$ is mapped onto the left of the interval $[-\frac{1}{2},0]$.
In general, the linear transformation $T(x)=ax$ stretches objects to change their length by a factor of $|a|$. If $a$ is positive, $T$ preserves the orientation; if $a$ is negative, $T$ reverses orientation. We will obtain similar conclusions for higher-dimensional linear transformations in terms of the determinant of the associated matrix.
Two-dimensional linear transformations
A two-dimensional linear transformation is a function $\vc{T}: \R^2 \to \R^2$ of the form $$\vc{T}(x,y) = (ax+by,cx+dy) = \left[\begin{array}{cc}a &b\\ c &d\end{array}\right]\left[\begin{array}{c}x\\y\end{array}\right],$$ where $a$, $b$, $c$, and $d$ are numbers defining the linear transformation. We can write this more succinctly as $$\vc{T}(\vc{x}) = A\vc{x},$$ where $\vc{x}=(x,y)$ and $A$ is the $2 \times 2$ matrix containing the constants that define the linear transformation, $$A = \left[\begin{array}{cc}a &b\\ c &d\end{array}\right].$$ We will view $\vc{T}$ as mapping objects from the $xy$-plane onto an $x'y'$-plane: $(x',y')=\vc{T}(x,y)$. As in the one-dimensional case, the geometric properties of this mapping will be reflected in the determinant of the matrix $A$ associated with $\vc{T}$.
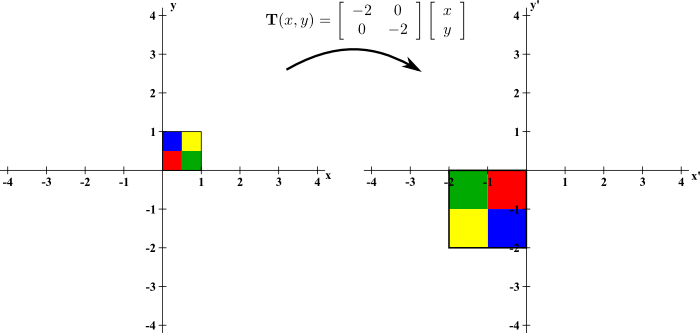
To begin, we look at the linear transformation $$\vc{T}(x,y) = \left[\begin{array}{cc}-2 &0\\ 0 &-2\end{array}\right]\left[\begin{array}{c}x\\y\end{array}\right].$$ As with all linear transformations, it maps the origin $\vc{x}=(0,0)$ back to the origin $(0,0)$. We can get a feel for the behavior of $\vc{T}$ by looking at its action on the standard unit vectors, $\vc{i}=(1,0)$ and $\vc{j}=(0,1)$. $\vc{T}$ maps $(1,0)$ to $(-2,0)$, and it maps $(0,1)$ to $(0,-2)$. It stretched both vectors by a factor of $2$ and rotated them all the way around by $\pi$ radians.
To better visualize the mapping of $\vc{T}$, we can examine how it maps a region in the plane. The below figure shows the mapping of $(x',y')=\vc{T}(x,y)$ on the unit square $[0,1] \times [0,1]$. We colored the quarters of the square in different colors to help visualize how points within the square were mapped. The figure demonstrates that $\vc{T}$ did rotate the square by $\pi$ radians around the origin and stretched each side by a factor of 2.
We claimed this behavior should be reflected in the determinant of the associated matrix $$A = \left[\begin{array}{cc}-2 &0\\ 0 &-2\end{array}\right].$$ In this case, $\det(A) = (-2)(-2)-(0)(0) = 4$. The determinant is 4 even though it seemed it was streching everything by a factor of 2. And the determinant was positive even though it rotated everything so that points on the right are mapped to points on left and points on the top are mapped to points on the bottom. Shouldn't we have gotten a negative determinant?
The reason for getting a factor of 4 rather than 2 is due to the fact that determinants of $2 \times 2$ matrices reflect area not length. In fact, the absolute value of the determinant of a $2 \times 2$ matrix \begin{align*} \left[ \begin{array}{cc} a_1 & a_2\\ b_1 & b_2 \end{array} \right] \end{align*} gives the area of the parallelogram spanned by the vectors $(a_1,a_2)$ and $(b_1,b_2)$. The mapping $\vc{T}$ stretched a $1 \times 1$ square of area 1 into a $2 \times 2$ square of area 4, quadrupling the area. This quadrupling of the area is reflected by a determinant with magnitude 4.
The reason for a positive determinant is that, in two-dimensions, rotations, even all the way around by $\pi$ radians, is not considered changing the orientation. If we go counterclockwise around the perimeter of the mapped square, we still encounter the colors in the order red, green, yellow, blue. Changing orientation would correspond to taking the square out of the $xy$-plane and flipping it before putting it down in the $x'y'$-plane, as we'll see in the next example.
The linear transformation $$\vc{T}(\vc{x}) = A\vc{x}, \qquad A = \left[\begin{array}{cc}-1 &-1\\ 1 &3\end{array}\right]$$ should change orientation as $\det(A) = (-1)(3)-(-1)(1) = -2$. It should also increase area by a factor of $|\det(A)| = 2$.
Again, we visualize the transformation $\vc{T}$ by looking at how it maps the unit square $[0,1] \times [0,1]$. As shown below, it maps the square into a parallelogram. Inspection of the paralleogram reveals that it indeed has area 2, so $\vc{T}$ doubles area as claimed. the orientation is also reversed. Moving counterclockwise around the perimeter of the parallelogram leads to the opposite color order red, blue, yelow, green. There is no way to stretch and move the original unit square into the parallelogram without taking it out of the plane and flipping it (or somehow moving the region through itself).
The actual geometric shape and rotation of the square's image is not captured by the determinant. We cannot tell whether or not $\vc{T}$ will map the square into a square, rectangle, rhombus, or other parallelogram from knowledge of just the determinant of its associate matrix. (We know it has to be some type of parallelogram, as all two-dimensional linear transformations do map parallelograms into parallelograms.) The determinant simply tells us how $\vc{T}$ changes area and whether or not it reverses orientation.
You can experiment with these and other linear transformations using the below applet. You can convince yourself that $\vc{T}$ always maps parallelograms onto parallelograms and that the determinant of its associated matrix does capture area stretching and orientation reversing.
Linear transformation in two dimensions. The linear transformation $\vc{T}=A\vc{x}$, with $A$ specified in the upper left hand corner of the applet, is illustrated by its mapping of a quadrilateral. The original quadrilateral is shown in the $xy$-plane of the left panel and the mapped quadrilateral is shown in the $x'y'$-plane of the right panel. You can change the linear transformation by typing in different numbers and change either quadrilateral by moving the points at its corners. The determinant of $A$ (shown in upper left hand corner) determines how much $\vc{T}$ stretches or compresses area and whether or not it reverses the orientation of the region. The orientation of each quadrilateral can be determined by examining the order of the colors while moving in a counterclockwise direction around its perimeter. Use the + and - buttons of each panel to zoom in and out. (When $\det A =0$, you cannot drag points in the right panel.)
Three-dimensional linear transformations
The reflection of geometric properties in the determinant associated with three-dimensional linear transformations is similar. A three-dimensional linear transformation is a function $\vc{T}: \R^3 \to \R^3$ of the form $$\vc{T}(x,y,z) = (a_{11}x+a_{12}y + a_{13}z, a_{21}x+a_{22}y+a_{23}z,a_{31}x+a_{32}y+a_{33}z) = A\vc{x}.$$ where $$A=\left[\begin{array}{ccc}a_{11}&a_{12}&a_{13}\\a_{21}&a_{22}&a_{23}\\a_{31}&a_{32}&a_{33}\end{array}\right]$$ and $\vc{x}=(x,y,z)$. The components $a_{ij}$ of $A$ define the linear transformation.
As above, the determinant $\det(A)$ reflects some of the geometric properties of the mapping $(x',y',z')=\vc{T}(x,y,z)$. Due to the fact that the absolute value of a determinant gives the volume of a parallelepiped, the absolute value $|\det(A)|$ reflects how much $\vc{T}$ expands volume. The sign of $\det(A)$ reflects whether or not $A$ preserves orientation, as above. If the $\det(A)$ is positve, the associated linear transformation preserves orientation in that it only stretches and rotates objects. On the other hand, if $\det(A)$ is negative, the associated linear transformation reverses orientation by also reflecting the object (taking its mirror image).
We illustrate with two examples. The first is the linear transformation associated with the matrix $$A=\left[\begin{array}{rrr}2&1&1\\1&2&-1\\-3&-1&2\end{array}\right].$$ Since $\det(A) = 12$, the linear transformation $\vc{T}(\vc{x}) = A\vc{x}$ expands the volume of objects by a factor of 12. Since the determinant is positive, it preserves the orientation of objects.
The action of $\vc{T}$ on the unit cube $[0,1] \times [0,1] \times [0,1]$ is illustrated in the following applet. $\vc{T}$ rotated the cube and stretched it into a parallelepiped of volume 12. You can confirm that $\vc{T}$ preserved orientation by comparing faces that have the same four colors and checking if the colors have the same order when moving counterclockwise. Since both the cube and the parallelepiped have faces with colors ordered red, yellow, white, magenta as one moves counterclockwise, the linear transformation preserved orientation, as it must given that $\det(A)$ is positive. You can change the cube into other parallelepipeds, and $\vc{T}$ always maps it to another parallelepiped, as it must.

Applet loading

Applet loading
A three-dimensional linear transformation that preserves orientation. The linear transformation $\vc{T}(\vc{x}) = A\vc{x}$, where $$A=\left[\begin{array}{rrr}2&1&1\\1&2&-1\\-3&-1&2\end{array}\right]$$ maps the unit cube to a parallelepiped of volume 12. The expansion of volume by $\vc{T}$ is reflected by that fact that $\det A = 12$. Since $\det A$ is positive, $\vc{T}$ preserves orientation, as revealed by the face coloring of the cube and parallelogram. The order of the colors on corresponding faces, when moving in a counterclockwise direction, is the same for both the cube and the parallelepiped. For example, both objects have a face with the counterclockwise color order blue, magenta, white, cyan. You can further explore the mapping by changing either shape to other parallelepipeds by dragging the points on four of its vertices.
Another example is the linear transformation associated with the matrix $$B=\left[\begin{array}{rrr}3&1&-3\\1&3&-2\\1&1&-3\end{array}\right].$$ Since $\det(B)=-14$, the linear transformation $\vc{T}=B\vc{x}$ stretches volume by the factor $|\det(B)| = 14$. In this case, since $\det(B)$ is negative, the linear transformation reverses orientation. The reversal of orientation can be seen in the below applet illustrating the mapping of the unit cube $[0,1] \times [0,1] \times [0,1]$. $\vc{T}$ maps the cube into a parallelepiped of volume $14$, but also reflects the cube in the process. This reversal of orientation can be observed by noticing that the parallelepiped has a face with the colors in the reverse order red, magenta, white, yellow, when moving counterclockwise.

Applet loading

Applet loading
A three-dimensional linear transformation that reverses orientation. The linear transformation $\vc{T}=B\vc{x}$, with $$B=\left[\begin{array}{rrr}3&1&-3\\1&3&-2\\1&1&-3\end{array}\right]$$ maps the unit cube to a parallelepiped of volume 14. The expansion of volume is reflected by the determinant $\det B = -14$. Since $\det B$ is negative, $\vc{T}$ not only expands volume by a factor of 14 but also reverse orientation, i.e., reflects objects into their mirror image. The reversal of orientation can be observed through the order of the colors on corresponding faces of the cube and parallelepiped. For example, the cube has a face with the colors ordered black, red, magenta, blue, when moving counterclockwise, while the parallelepiped has a face with the counterclockwise color order black, blue, magenta, red. You can further explore the mapping by changing either shape to other parallelepipeds by dragging the points on four of its vertices.
Thread navigation
Vector algebra
- Previous: The relationship between determinants and area or volume
- Next: Geometric properties of the determinant
Math 2374
Similar pages
- Geometric properties of the determinant
- Matrices and determinants for multivariable calculus
- Linear transformations
- Area calculation for changing variables in double integrals
- Length, area, and volume factors
- Polar coordinates mapping
- Volume calculation for changing variables in triple integrals
- How linear transformations map parallelograms and parallelepipeds
- Matrices and linear transformations
- The relationship between determinants and area or volume
- More similar pages