Image: A parallelogram
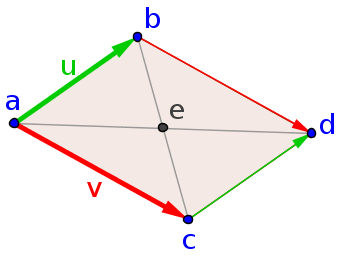A parallelogram is a quadrilateral whose opposites sides are parallel. This parallelogram is spanned by the vectors $\vc{u}$ and $\vc{v}$ with one vertex at the point $\vc{a}$. The fact that the quadrilateral is a parallelogram can be seen by the condition that the fourth vertex $\vc{d}$ is equal to $\vc{a}+\vc{u}+\vc{v}$, given that the other two vertices are $\vc{b}=\vc{a}+\vc{u}$ and $\vc{c}=\vc{a}+\vc{v}$. This condition can be rewritten in terms of the vertices alone as $\vc{d}=\vc{b}+\vc{c}-\vc{a}$ or $\vc{a}+\vc{d}=\vc{b}+\vc{c}$. Hence, the midpoints between the opposite vertices $(\vc{a}+\vc{d})/2$ and $(\vc{b}+\vc{c})/2$ must be the same point, which is labeled as $\vc{e}$.
Image file: parallelogram.png
Source image file: parallelogram.ggb
Source image type: Geogebra
Image links
This image is found in the pages