Image: Volume of parallelepiped
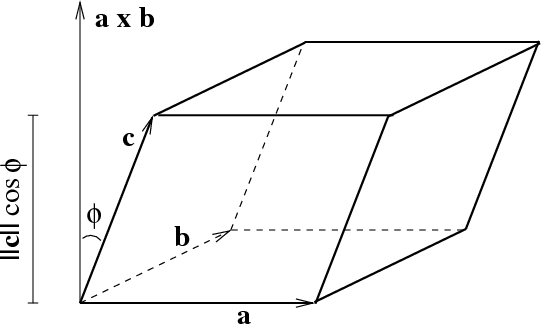The volume of the parallelepiped spanned by $\vc{a}$, $\vc{b}$, and $\vc{c}$ is
\begin{align*}
\text{Volume} &= \text{area of base} \cdot \text{height}\\
&= \|\vc{a} \times \vc{b}\| ~ \|\vc{c}\| ~ |\cos
\phi | = |(\vc{a} \times \vc{b}) \cdot \vc{c}|.
\end{align*}
The formula results from properties of the cross product: the area of the parallelogram base is $\|\vc{a} \times \vc{b}\|$ and the vector $\vc{a} \times \vc{b}$ is perpendicular to the base. The height of the parallelepiped is $\|\vc{c}\| ~ |\cos \phi |$. The angle $\phi$ between $\vc{c}$ and $\vc{a} \times \vc{b}$ could be larger than $\pi/2$, depending on the order of $\vc{a}$ and $\vc{b}$, so we must take the absolute value in the definition of the volume.
Image file: volume_parallelepiped.png
Image links
This image is found in the pages