The scalar triple product
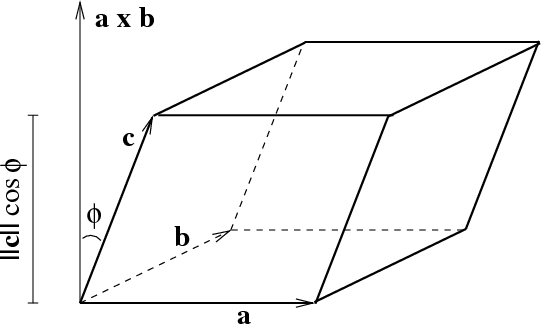
The scalar triple product of three vectors $\vc{a}$, $\vc{b}$, and $\vc{c}$ is $(\vc{a} \times \vc{b}) \cdot \vc{c}$. It is a scalar product because, just like the dot product, it evaluates to a single number. (In this way, it is unlike the cross product, which is a vector.) The scalar triple product is important because its absolute value $|(\vc{a} \times \vc{b}) \cdot \vc{c}|$ is the volume of the parallelepiped spanned by $\vc{a}$, $\vc{b}$, and $\vc{c}$ (i.e., the parallelepiped whose adjacent sides are the vectors $\vc{a}$, $\vc{b}$, and $\vc{c}$).
This formula for the volume can be understood from the above figure. The volume of the parallelepiped is the area of the base times the height. From the geometric definition of the cross product, we know that its magnitude, $\|\vc{a} \times \vc{b}\|$, is the area of the parallelogram base, and that the direction of the vector $\vc{a} \times \vc{b}$ is perpendicular to the base. The height of the parallelepiped is the component of $\vc{c}$ in the direction normal to the base, i.e., in the direction of $\vc{a} \times \vc{b}$. Hence the height is $ \|\vc{c}\| ~ |\cos \phi |$, where $\phi$ is the angle between $\vc{c}$ and $\vc{a} \times \vc{b}$. (Why do we need the absolute value? If we swapped the locations of $\vc{a}$ and $\vc{b}$, in the above figure, then $\vc{a} \times \vc{b}$ would point downward. The angle $\phi$ would be larger than $\pi/2$, and $\cos\phi$ would be negative.)
The volume of the parallelepiped is therefore \begin{align*} \text{Volume} = \|\vc{a} \times \vc{b}\| ~ \|\vc{c}\| ~ |\cos \phi | = |(\vc{a} \times \vc{b}) \cdot \vc{c}|. \end{align*} (Remember the definition of the dot product.) Using the formula for the cross product in component form, we can write the scalar triple product in component form as \begin{align*} (\vc{a} \times \vc{b}) \cdot \vc{c} &= \left| \begin{array}{cc} a_2 & a_3\\ b_2 & b_3 \end{array} \right| c_1 - \left| \begin{array}{cc} a_1 & a_3\\ b_1 & b_3 \end{array} \right| c_2 + \left| \begin{array}{cc} a_1 & a_2\\ b_1 & b_2 \end{array} \right| c_3 \\ &= \left| \begin{array}{ccc} c_1 & c_2 & c_3\\ a_1 & a_2 & a_3\\ b_1 & b_2 & b_3 \end{array} \right|. \end{align*}
The below applet can help you understand the properties of the scalar triple product $(\vc{a} \times \vc{b}) \cdot \vc{c}$. It includes the outline of the parallelepiped spanned by these vectors, whose volume is $|(\vc{a} \times \vc{b}) \cdot \vc{c}|$, as well as the vector corresponding to the cross product $\vc{a} \times \vc{b}$. (Apologies to color blind people for reliance on colors in this applet.)
The scalar triple product can be positive, negative, or zero. (That's why we need the absolute value for the volume.) What determines the sign of $(\vc{a} \times \vc{b}) \cdot \vc{c}$? Also, when $(\vc{a} \times \vc{b}) \cdot \vc{c}=0$, what is going on? (If you rotate the graph once you've made scalar triple product zero, you'll immediately see that answer.)
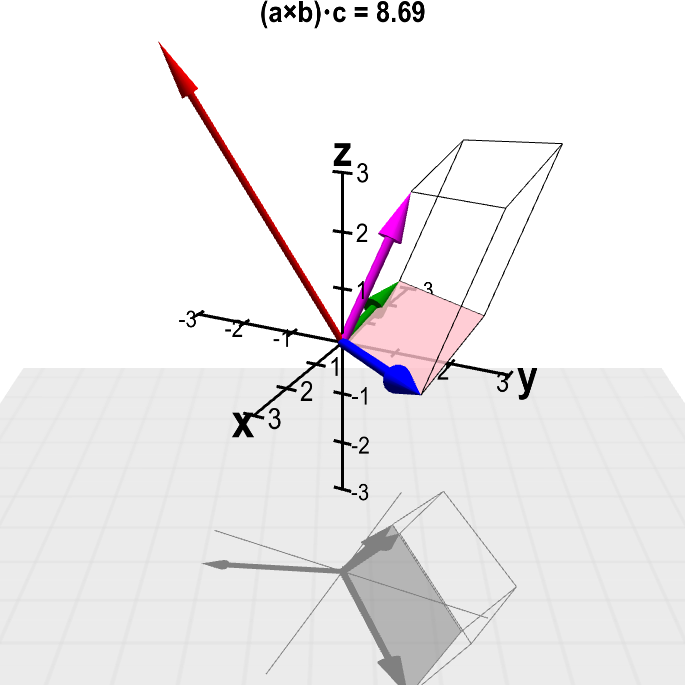
Applet loading
Scalar triple product. The value of the scalar triple product $(\color{blue}{\vc{a}} \times \color{green}{\vc{b}}) \cdot \color{magenta}{\vc{c}}$ is shown at the top, where the vectors $\color{blue}{\vc{a}}$ (in blue), $\color{green}{\vc{b}}$ (in green), and $\color{magenta}{\vc{c}}$ (in magenta) can changed by dragging their tips with the mouse. The volume of the spanned parallelepiped (outlined) is the magnitude $\|(\color{blue}{\vc{a}} \times \color{green}{\vc{b}}) \cdot \color{magenta}{\vc{c}}\|$. The cross product $\color{blue}{\vc{a}} \times \color{green}{\vc{b}}$ is shown by the red vector; its magnitude is the area of the highlighted parallelogram, which is one face of the parallelepiped.
The three-dimensional perspective of this graph is hard to perceive when the graph is still. If you keep the figure rotating by dragging it with the mouse, you'll see it much better.
In case you like to see it with numbers, here's an example of calculating the volume of a parallelepiped using the scalar triple product.
Do we care about parallelepipeds?
The scalar triple product is obviously very useful if you have a lot of parallelepipeds lying around and want to know their volume. But, if you don't happen to find yourself pining to know the volume of a parallelepiped, you may wonder what's the use of the scalar triple product.
To begin with, we recommend you first master the cross product. If you have only enough available brain cells to master either the cross product or the scalar triple product, we'd recommend focusing on the cross product. Its applications are more immediate, and its use is more widespread.
Nonetheless, the scalar triple product does have its uses even if you aren't that excited about parallelepipeds. In multivariable calculus, it turns out there are parallelepipeds lurking behind some important formulas and theorems. The reason stems from the definition of the differentiability of functions. In a nutshell, differentiability means that a function looks linear if you zoom in. Calculus is all about the infinitesimal (i.e., making everything small), so the small structure you see when zooming in is fundamental. Bottom line of this: linear functions are fundamental in calculus.
The route to parallelepipeds comes through these linear functions, which we'll call linear transformations or linear maps to emphasize how they map objects into other objects. It turns out that three-dimensional linear transformations always map parallelepipeds into other parallelepipeds. Thus, properties of linear maps can be seen by how they transform parallelepipeds. One of these properties is how linear maps expand or contract objects. Here comes the scalar triple product, as it measures the volume that is changing. In particular, the above determinant form of the scalar triple product is key, as matrices are strongly linked to linear transformations.
If you find this linear transformation business too abstract to help you appreciate the utility of the scalar triple product, you could also think about triple integrals, whose definition is based on chopping up a region into small boxes. If you are thinking that a box is a type of parallelepiped and small means a linear transformation is relevant, then you definitely need to get out more and do other things besides think about math. But those connections are exactly how the scalar triple product gets tied to triple integrals. We don't need a scalar triple product for a regular triple integral, though, as we know how to calculate the volume of a box without it. But, when you start changing variables in triple integrals, then the box gets transformed into a parallelepiped, and the scalar triple product volume calculation becomes important.
Thread navigation
Vector algebra
- Previous: Cross product examples
- Next: Scalar triple product example
Math 2374
- Previous: Cross product examples
- Next: Scalar triple product example
Similar pages
- Scalar triple product example
- The cross product
- Cross product examples
- The formula for the cross product
- The dot product
- The formula for the dot product in terms of vector components
- Dot product examples
- The relationship between determinants and area or volume
- Multiplying matrices and vectors
- Matrix and vector multiplication examples
- More similar pages