Applet: Cobwebbing and linear approximations around equilibria
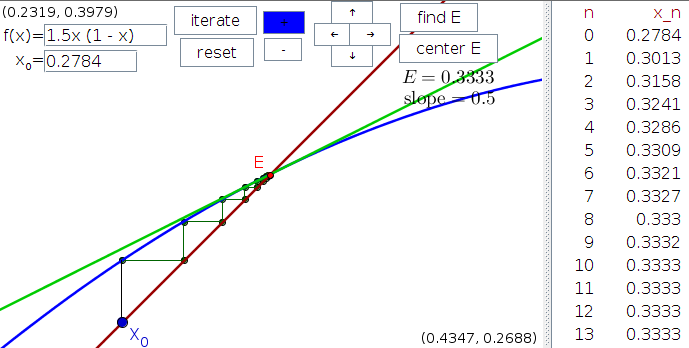
Cobwebbing provides a way to visualize how a linear approximation to a function captures the behavior of its iteration near equilibria. Clicking the “iterate” button shows the behavior of the function iteration $x_n = f(x_{n-1})$ in a cobweb plot. The iterates $x_n$ are also displayed in the list at the right. To find an equilibrium (defined by $E=f(E)$), click the “find E” button, then click near a point where the graph of $f(x)$ (blue curve) intersects the diagonal $y=x$ (red line). If an equilibrium is found, the value of $E$ is displayed and a red point appears at the coordinates $(E,E)$. The linear approximation of $f$ around $E$ appears as a green line that is tangent to the graph of $f$ at the red point, and the value of its slope is displayed. If you click “center E,” the red point representing $E$ will be centered, and you can zoom in with the + button to see the behavior of $f$ right around $E$. What do you notice about the relationship of the linear approximation in green and the function in blue when you zoom in on the equilibrium? What does this say about the ability of the linear approximation to predict the behavior of $f$ around $E$?
You can change the function $f(x)$ by typing a new function in the box. You can change the initial point $x_0$ by typing a new value in the box or dragging the blue point. You can zoom in and out with the + and - buttons as well as pan in different directions with the buttons labeled by arrows.
Applet file: cobweb_linear_approximation_equilibrium.ggb
Applet links
This applet is found in the pages
General information about Geogebra applets
This applet was created using Geogebra. In most Geogebra applets, you can move objects by dragging them with the mouse. In some, you can enter values with the keyboard. To reset the applet to its original view, click the icon in the upper right hand corner.
Since these applets use Java, you must have Java installed and properly configured in your browser for the them to display. You can get Java here.
You can download the applet onto your own computer so you can use it outside this web page or even modify it to improve it. You simply need to download the above applet file and download the Geogebra program onto your own computer.