Applet: Divergent vector field with embedded sphere
Applet loading
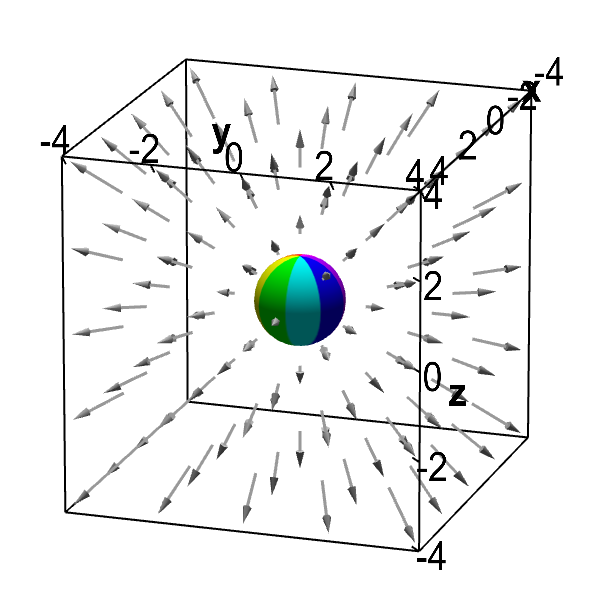
The sphere embedded in this vector field can be used to visualize the divergence of this vector field. If the vector field $\dlvf(x,y,z)$ indicates the velocity of a fluid at point $(x,y,z)$, then one can visualize how much fluid is flowing in and out of the sphere by the direction and length of the vectors.
When the sphere is at the origin, it is clear that fluid is moving out of the sphere. When the sphere is moved away from the origin, fluid flows into the side of the sphere closest to the origin, and fluid flows out of the side of the sphere further from the origin. Since the fluid speeds up as it gets further from the origin (indicated by the increasing length of the vectors), the fluid is flowing out of the sphere at a greater velocity than it is flowing in. In addition, since the velocity field is radiating outward, fluid is flowing out of the sphere over more than half of its surface. This visualization suggests that more fluid is flowing out of the sphere than is flowing into the sphere, no matter the sphere's position. Hence, it appears the fluid may be expanding.
Indeed, the vector field does have a positive divergence. The vector field is $\dlvf(x,y,z) = (x,y,z)$. Its divergence is $\pdiff{\dlvfc_1}{x}+\pdiff{\dlvfc_2}{y}+\pdiff{\dlvfc_3}{z}=1+1+1=3$. The vector field has a constant, positive divergence everywhere.
Applet links
This applet is found in the pages
General information about three.js applets
The applet was made using three.js and requires Javascript as well as a browser that supports WebGL. For most three.js applets, you can drag with the mouse to rotate the view, drag with the right button to pan, and zoom in/out with the mouse wheel. Many applets contain points that you can drag to change values of variables.