Applet: A rotating sphere indicating the presence of curl
Applet loading
Applet loading
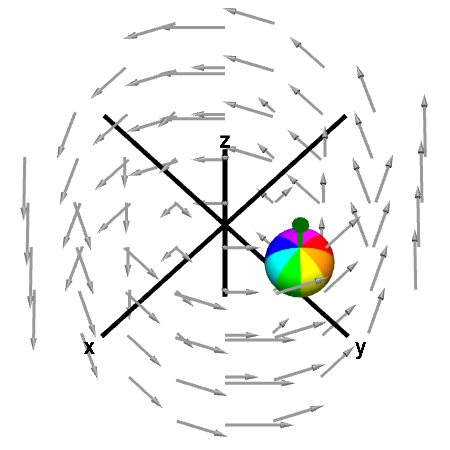
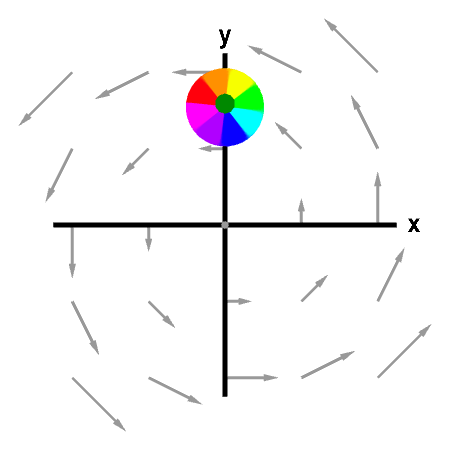
The rotation of the sphere when its center is fixed in an indication of the curl of the vector field. The curl of the vector field is shown by the green arrow. First panel shows the full vector field; second panel shows its projection in the $xy$-plane. You can move the sphere by dragging it with the mouse.
This vector field is $\dlvf(x,y,z)= (-y,x,0).$ Its curl is \begin{align*} \curl \dlvf(x,y,z) &= \left(\pdiff{}{y}0-\pdiff{}{z}x, \pdiff{}{z}(-y)- \pdiff{}{x}0, \pdiff{}{x}x - \pdiff{}{y}(-y) \right)\\ &=(0,0,2), \end{align*} which is a constant independent of point $(x,y,z)$ and always points in the positive $z$ direction. Therefore, the rotation of the sphere is unchanged as you move it around.
Applet links
This applet is found in the pages
General information about three.js applets
The applet was made using three.js and requires Javascript as well as a browser that supports WebGL. For most three.js applets, you can drag with the mouse to rotate the view, drag with the right button to pan, and zoom in/out with the mouse wheel. Many applets contain points that you can drag to change values of variables.