Subtleties about curl
Macroscopic versus microscopic circulation
We introduced the curl of a vector field as the microscopic circulation of the vector field. In that introductory reading we attempted to keep things as simple as possible, so we didn't make a big fuss over the difference between macroscopic circulation of the vector around in circles and the microscopic circulation that curl measures. For the example vector field we showed, the microscopic and macroscopic circulations were essentially the same, so we didn't have to worry about the difference between them.
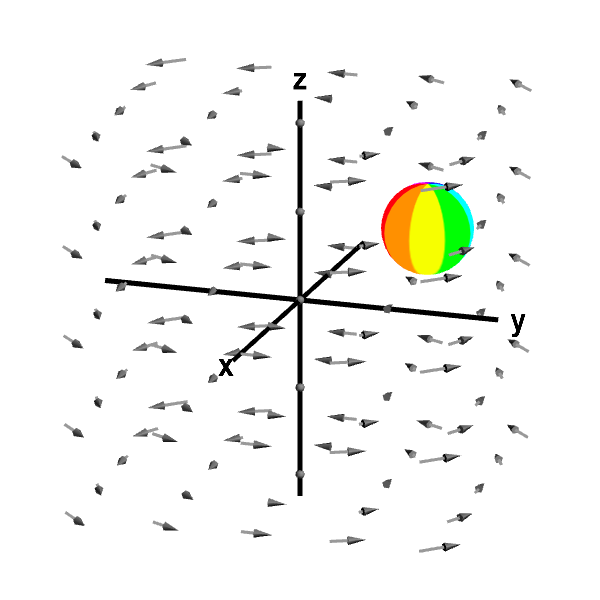
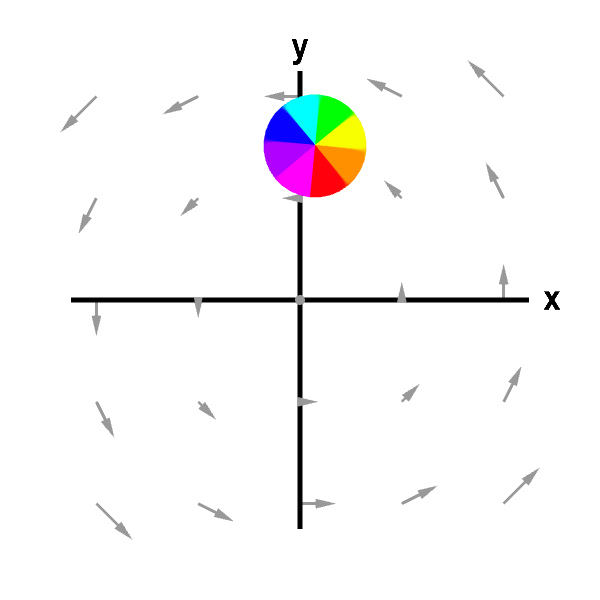
The vector field $\dlvf(x,y,z) = (-y,x,0)$ is similar to the vector field of the introductory reading except that the rotation is around the $z$-axis. In this case, the macroscopic circulation is counterclockwise when viewed from the positive $z$-axis. In this case, we can see circulation by placing a sphere in the fluid and allowing it to move freely with the fluid. (Unfortunately, this method doesn't always work.) The macroscopic circulation is evident by the sphere's circling around the $z$-axis. Since this vector field has no $z$-component and is independent of $z$, we may be able to get a better picture of the action by looking at the projection in the $xy$-plane, viewed from the positive $z$-axis, which is shown to the right. In all the examples on this page, we'll use vector fields with this property, and each figure will show the three-dimensional graph at the left along with its two-dimensional projection at the right.
Applet loading
Applet loading
Circling sphere in rotating vector field. The sphere is circulating around the $z$-axis due to the macroscopic circulation of the fluid flow described by the vector field. This macroscopic circulation, however, is not a measurement of the curl of the vector field. First panel shows the full vector field; second panel shows its projection in the $xy$-plane.
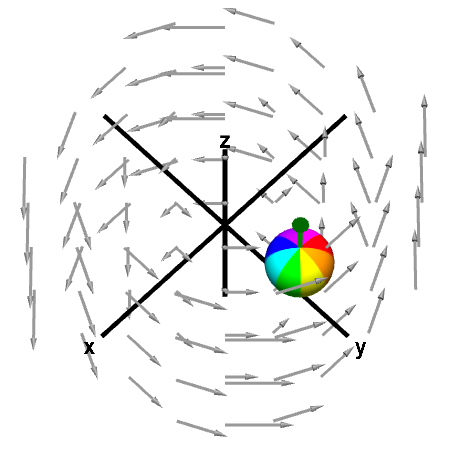
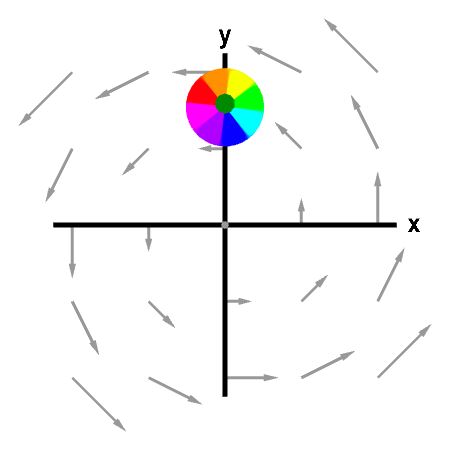
It is important to remember that this macroscopic circulation isn't the curl of the vector field. Recall that in order to measure the microscopic circulation of the curl, one needs to fix the center of the sphere and allow it to rotate freely around the center. In this example, there is nothing tricky, and the rotation is again counterclockwise when viewed from the positive $z$-axis. Using the right hand rule, the curl points in the positive $z$ direction, as shown by the green arrow. Indeed, $\curl \dlvf = (0,0,2)$.
Applet loading
Applet loading
A rotating sphere indicating the presence of curl. Since the center of the sphere is fixed, this rotation is indeed an indication of the vector field's curl, which is indicated by the green arrow. First panel shows the full vector field; second panel shows its projection in the $xy$-plane. You can move the sphere by dragging it with the mouse. Since for this particular vector field, the curl does not change with position, the rotation of the sphere is unchanged as you move it around.
However, you may or may not be surprised to learn that for some vector fields, the microscopic and macroscopic circulations could be quite different. The definition of curl as microscopic circulation is a little more subtle than it just being a measure of the rotation of the vector field.
Curl-free macroscopic circulation
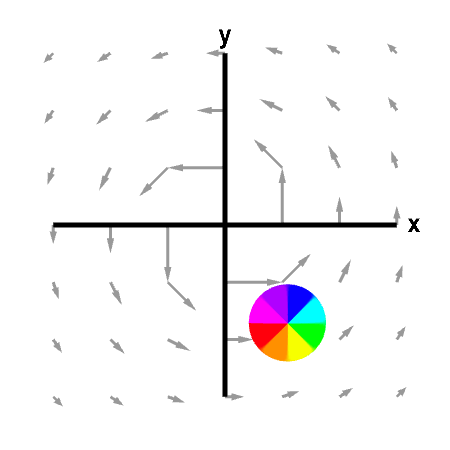
In the vector field pictured below, there is clear macroscopic circulation of the vector field around the $z$-axis. If we placed a sphere in a fluid with velocity given by the vector field, and allowed the sphere to move freely with the fluid, it would circulate around the $z$-axis as shown.

Applet loading
Applet loading
Circling sphere in a vector field with zero curl. The sphere is circulating around the z-axis due to the macroscopic circulation of the fluid flow described by the vector field. However, this fluid has no microscopic circulation, as its curl is zero. First panel shows the full vector field; second panel shows its projection in the xy-plane.
Does this circulation correspond to the microscopic circulation of curl? Again, one needs to fix the center of the sphere to measure curl, as the motion of a free-floating sphere does not correspond to curl. If the sphere still spins when its center is fixed, such spinning around its center would measure the microscopic circulation of curl (at least if the sphere were very small). As shown below, the sphere with its center fixed does not rotate, indicating the absence of curl.

Applet loading

Applet loading
A nonrotating sphere indicating absence of curl. Although the fluid represented by this vector field is circulating around the $z$-axis, the sphere does not rotate when its centered is fixed to a single point. This lack of rotation indicates that the curl is zero; this fluid has no microscopic circulation. First panel shows the full vector field; second panel shows its projection in the xy-plane.
This vector field is $$\dlvf(x,y,z) = \frac{(-y,x,0)}{x^2+y^2}$$ for $(x,y) \ne (0,0)$. Along circles $x^2+y^2=$ constant, the vector field is similar to the first vector field, above, giving the vector field the macroscopic circulation around the $z$-axis. However, due to the denominator, the vector field shrinks rapidly as one moves away from the $z$-axis. Since for $(x,y) \ne (0,0)$, $$\pdiff{\dlvfc_2}{x} =\pdiff{\dlvfc_1}{y}= \frac{y^2-x^2}{(x^2+y^2)^2}$$ one can compute that away from the $z$-axis, $\curl \dlvf(x,y,z) = (0,0,0)$.
How can one see from the picture that the microscopic circulation is zero? The general rotation of the flow around the $z$-axis in the counterclockwise direction (as viewed from the positive $z$-axis) would indeed tend to make the sphere spin in that direction. But, since the arrows are longer closer to the $z$-axis, the vector field tends to push the sphere more strongly on the side closest to the $z$-axis. This second effect would tend to make the sphere spin in the clockwise direction (viewed from the positive $z$-axis). In this example, I have chosen the vector field so that the two effects precisely cancel each other out so that the curl is zero.
Curl that is opposite of macroscopic circulation
Of course, the effects need not balance. For the vector field $$\dlvf(x,y,z) = \frac{(-y,x,0)}{(x^2+y^2)^{3/2}},$$ for $(x,y) \ne (0,0)$, the length of the arrows diminishes even faster as one moves away from the $z$-axis. In this case, the microscopic circulation is opposite of the macroscopic circulation, and the sphere with a fixed center rotates clockwise (when viewed from the positive $z$-axis), as shown below. Using the right hand rule, $\curl \dlvf$ must point downward, as shown by the green arrow. We can calculate that for $(x,y) \ne (0,0)$, $$\curl \dlvf(x,y,z) = \frac{(0,0,-1)}{(x^2+y^2)^{3/2}}.$$

Applet loading

Applet loading
Sphere rotating in opposite direction of macroscopic circulation. The fluid represented by this vector field is circulating in a counterclockwise when viewed from the positive $z$-axis. On the other hand, the sphere with its center fixed is rotating in a clockwise direction. This rotation indicates that the curl is pointing downward, as shown by the green arrow. First panel shows the full vector field; second panel shows its projection in the xy-plane. The vector field and its curl blow up near the $z$-axis (the vector field arrows would get much longer if we plotted then closer to the $z$-axis). Hence, the sphere spins faster and the curl vector grows longer, the closer you move the sphere to the $z$-axis.
Circulation may not be obvious from pictures
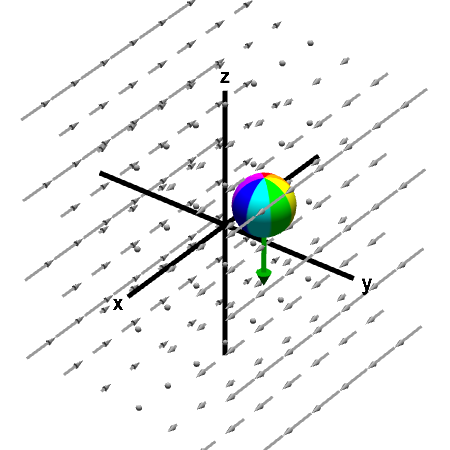
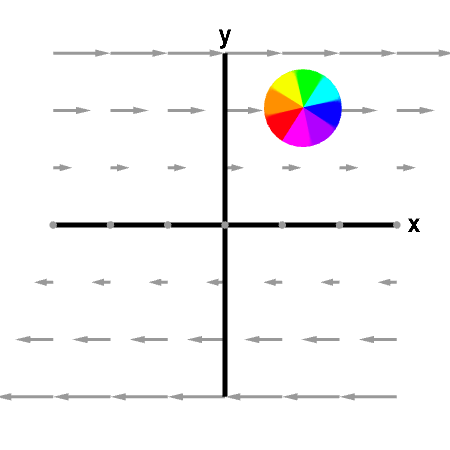
For the vector field $\dlvf(x,y,z) = (y,0,0)$, no rotation is readily apparent, as the vector field is always parallel to the $x$-axis. However, if we place a sphere in the flow and fix its center, it does indeed spin. The spin is clockwise when viewed from the positive $z$-axis, so the curl points in the negative $z$ direction as shown by the green arrow. Indeed, one can easily calculate that $\curl \dlvf(x,y,z) = (0,0,-1)$.
Applet loading
Applet loading
Sphere rotating in shear flow. Even though the fluid flow represented by this vector field does not seem to be rotating, the rotating sphere demonstrates that there is microscopic circulation. The curl points downward, as shown by the green arrow. First panel shows the full vector field; second panel shows its projection in the xy-plane. You can move the sphere by dragging it with the mouse. Since for this particular vector field, the curl does not change with position, the rotation of the sphere is unchanged as you move it around.
The sphere spins because the flow on the positive $y$ side the sphere pushes the sphere more strongly in the positive $x$ direction, compared with the flow on the negative $y$ side of the sphere.
In this case, the subtle issue isn't between microscopic and macroscopic circulation. The macroscopic circulation, as one might define it via line integrals, would also be clockwise when viewed from the positive $z$ axis. Since such macroscopic circulation cannot be measured by letting a sphere float freely in the flow, this example shows how measuring macroscopic circulation with spheres doesn't always work.
Thread navigation
Multivariable calculus
- Previous: The idea of the curl of a vector field
- Next: The components of the curl
Math 2374
- Previous: Subtleties about divergence
- Next: The components of the curl
Similar pages
- The idea of the curl of a vector field
- The components of the curl
- A path-dependent vector field with zero curl
- Subtleties about divergence
- Divergence and curl notation
- Divergence and curl example
- The idea behind Green's theorem
- The definition of curl from line integrals
- Calculating the formula for circulation per unit area
- The idea behind Stokes' theorem
- More similar pages