Graph definition
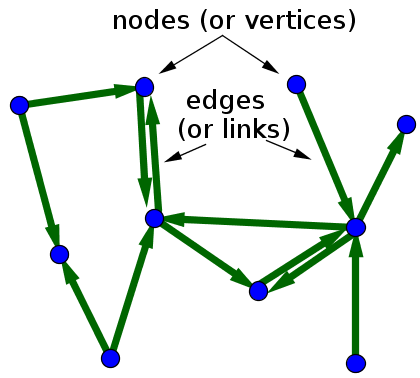
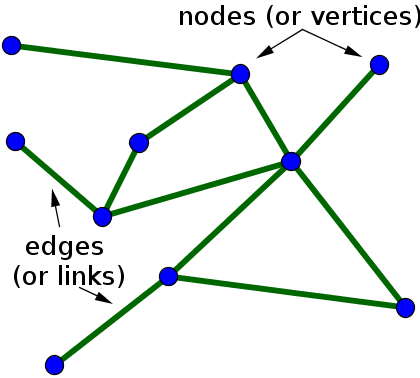
The term graph can refer to two completely different things. Students usually first learn of a graph as plot of a function, or a function graph. Here, we refer to a different definition of graph, in which a graph is another word for a network, i.e., a set of objects (called vertices or nodes) that are connected together. The connections between the vertices are called edges or links.
If the edges in a graph are directed, i.e., pointing in only one direction, the graph is called a directed graph, or sometimes digraph for short. When drawing a directed graph, the edges are typically drawn as arrows indicating the direction, as illustrated in the first figure, below. If all edges are bidirectional, or undirected, the graph is an undirected graph, as illustrated by the second figure.
One can formally define an undirected graph as $G= (\mathcal{N},\mathcal{E})$, consisting of the set $\mathcal{N}$ of nodes and the set $\mathcal{E}$ of edges, which are unordered pairs of elements of $\mathcal{N}$. The formal definition of a directed graph is similar, the only difference is that the set $\mathcal{E}$ contains ordered pairs of elements of $\mathcal{N}$.
For more information about graphs, see the network introduction.