Image: The curve used to derive a formula for the circulation per unit area
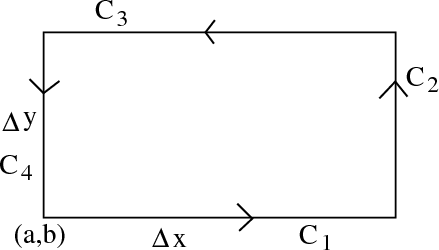The rectangular curve $\dlc$ used to derive a formula for the circulation per unit area
Image file: circulation_unit_area_calculation_curve.png
Image links
This image is found in the pages