Image: Marginal degree distributions of a directed network
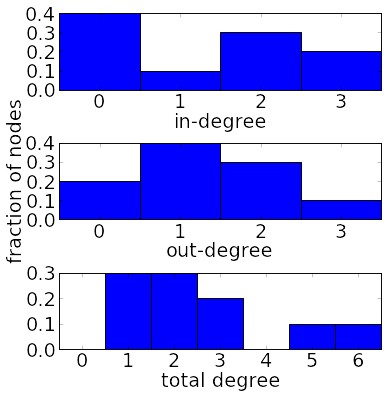
The marginal degree distributions and the total degree distribution of a directed network with 10 nodes and 13 links.
The network has adjacency matrix \begin{gather*} A \nobreak{=}\left[ \begin{array}{cccccccccc} 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0\\ 1 & 0 & 0 & 0 & 0 & 1 & 0 & 0 & 0 & 0\\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0\\ 0 & 0 & 0 & 0 & 0 & 0 & 1 & 0 & 0 & 0\\ 1 & 0 & 0 & 0 & 0 & 0 & 0 & 1 & 0 & 0\\ 0 & 1 & 0 & 0 & 0 & 0 & 1 & 1 & 0 & 0\\ 0 & 0 & 1 & 0 & 0 & 0 & 0 & 0 & 1 & 1\\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0\\ 0 & 0 & 0 & 0 & 0 & 1 & 1 & 0 & 0 & 0\\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \end{array} \right]. \end{gather*} Its in- and out- and total degrees are $k_1^{\text{in}}=0$, $k_1^{\text{out}}=2$, $k_1^{\text{tot}}=2$, $k_2^{\text{in}}=2$, $k_2^{\text{out}}=1$, $k_2^{\text{tot}}=3$, $k_3^{\text{in}}=0$, $k_3^{\text{out}}=1$, $k_3^{\text{tot}}=1$, $k_4^{\text{in}}=1$, $k_4^{\text{out}}=0$, $k_4^{\text{tot}}=1$, $k_5^{\text{in}}=2$, $k_5^{\text{out}}=0$, $k_5^{\text{tot}}=2$, $k_6^{\text{in}}=3$, $k_6^{\text{out}}=2$, $k_6^{\text{tot}}=5$, $k_7^{\text{in}}=3$, $k_7^{\text{out}}=3$, $k_7^{\text{tot}}=6$, $k_8^{\text{in}}=0$, $k_8^{\text{out}}=2$, $k_8^{\text{tot}}=2$, $k_9^{\text{in}}=2$, $k_9^{\text{out}}=1$, $k_9^{\text{tot}}=3$, $k_{10}^{\text{in}}=0$, $k_{10}^{\text{out}}=1$, $k_{10}^{\text{tot}}=1$.
Image file: small_directed_network_marginal_degree_distributions.png
Source image file: small_directed_network_marginal_degree_distributions.py
Source image type: Python
Image links
This image is found in the pages