Image: A 2D vector field pointing inward
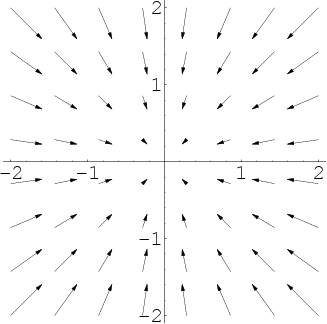This vector field illustrates compression or negative divergence. The vector field is $\dlvf(x,y)=(-x,-y)$. Its divergence is $\div \vc{\dlvf}=\pdiff{\dlvfc_1}{x}+\pdiff{\dlvfc_2}{y}=-1-1=-2$.
Image file: vector_field_implosion.png
Image links
This image is found in the pages