Math Insight

Solutions to elementary integral problems

Problem 1

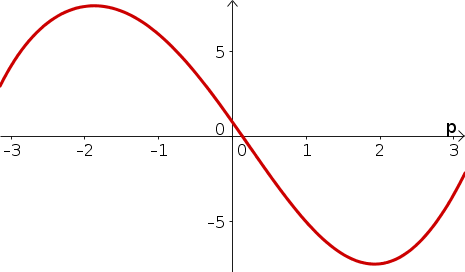
    1. $H(p)$ is increasing for $p \lt -1.8$ and $p \gt 1.8$, approximately.
    2. $H(p)$ is decreasing for $-1.8 \lt p \lt 1.8$, approximately.
  2. Below is a sketch of $H(p)$. (One could raise or lower the graph due to the arbitrary integration constant.)
Integral example function 1, with integral

Problem 2

  1. For what values of $z$ is $R(z)$
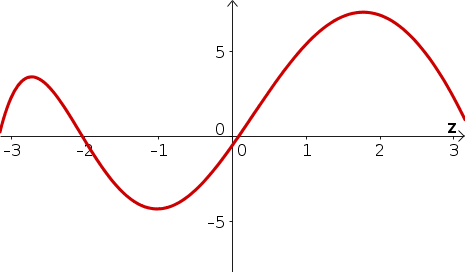
    1. $R(z)$ is increasing for $z \lt -2.7$ and $-1 \lt z \lt 1.7$, approximately.
    2. $R(z)$ is decreasing for $-2.7 \lt z \lt -1$ and $z \gt 1.7$, approximately.
  2. Below is a sketch of $R(z)$. (One could raise or lower the graph due to the arbitrary integration constant.)
Integral example function 2, with integral

Problem 3

\begin{align*} \int (3z^3-2/z^2-1)dz &= \frac{3}{4}z^4 + 2/z -z +c \end{align*}

Problem 4

One antiderivative of $h(u)=\sqrt{u}-e^u$ is $H(u)=\frac{2}{3}u^{3/2}-e^u$.

Problem 5

$$\int e^{-3t} dt = -\frac{1}{3}e^{-3t} + c.$$

Problem 6

One antiderivative of $g(t)= e^{-3t}$ is $G(t)= -\frac{1}{3}e^{-3t}$.

Problem 7

$m(t)= -\frac{1}{3}e^{-3t} +c$. Since $1=m(0)=-\frac{1}{3}e^{0} +c = -\frac{1}{3} +c$, the constant is $c=1+1/3=4/3$. The solution is $$m(t) = -\frac{1}{3}e^{-3t} + 4/3.$$

Problem 8

Since $\diff{}{t}(2t^2+t-5) = 1+4t$, one can integrate the right hand side of the equation to determine that $q(t)= e^{2t^2+t-5}+c$. Since $6=q(0)=e^{-5}+c$, the constant is $c=6-e^{-5}$, and the solution to the pure-time differential equation is $$q(t) = e^{2t^2+t-5} +6 -e^{-5}.$$

Problem 9

$$r(t) = \frac{1}{2}t^4 - 2t^3 +t^2/2-t + c.$$ Since $$3 = r(2) = 8-16+2-2+c=-8+c,$$ the constant is $c=11$, and the solution to the pure-time differential equation is $$r(t) = \frac{1}{2}t^4 - 2t^3 +t^2/2-t +11.$$

Problem 10

\begin{align*} \int_2^3 (1-x^2+x^{-1}) dx &= x - \frac{1}{3}x^3+\ln(x) \Big|_2^3\\ &= 3 - 9 + \ln(3) -(2-8/3+\ln(2)\\ &= -16/3 + \ln(3)-\ln(2)\\ &= -16/3 + \ln(3/2) \end{align*}

Problem 11

The average value of $f(z)=3z^2+7$ over the interval $[-1,2]$ is \begin{align*} \frac{1}{2-(-1)} \int_{-1}^2 (3z^2+7)dz &= \frac{1}{3}(z^3+7z)\Big|_{-1}^2 \\ &= \frac{1}{3}(8+14 - (-1-7))\\ &= 10 \end{align*}

Problem 12

The area under graph of $g(x)=2e^{-x}$ over the interval $[-1, 0]$ is \begin{align*} \int_{-1}^0 2e^{-x} dx &= -2e^{-x} \Big|_{-1}^0\\ &= -2e^{0} - (-2e^{1}) = 2e-2. \end{align*}

Problem 13

$V(t) = \frac{2}{3}t^{3/2}- t^3/120+c$. Since $V(0)=0$, the constant is $c=0$. The solution is $V(t) = \frac{2}{3}t^{3/2}- t^3/120$.

Problem 14

Since $\diff{}{t} (2t-t^2/4) = 2 - t/2$, the antiderivative is $p(t) = e^{2t-t^2/4}+c$. To determine the constant, we set $1=p(0)=e^{0}+c=1+c$, i.e., $c=0$. The share price at year $t$ is $p(t)=e^{2t-t^2/4}$. After one year, the share price is $p(1)=e^{7/4} \approx \$2.12$. After four years, the share price is $p(4) = e^{4} = \$54.60$. After ten years, the share price is $p(10)= e^{-5} \approx \$0.01$.

Problem 15

Using Forward Euler with $\Delta t = 0.5$, the time steps are $t_0=0$, $t_1=0.5$, $t_2=1$, $t_3=1.5$, and $t_4=2$. The solution is \begin{align*} h(2) &\approx 3 + \sum_{i=0}^3 e^{-t_i^2}\Delta t\\ &= 3+ e^{-0}0.5 + e^{-0.5^2}0.5 + e^{-1^2}0.5 + e^{-1.5^2}0.5\\ &\approx 4.126 \end{align*}

Problem 16

Using a left Riemann sum with $\Delta t= 0.5$, the subintervals are $t_0=0$, $t_1=0.5$, $t_2=1$, $t_3=1.5$, and $t_4=2$. The solution is \begin{align*} \int_0^2 e^{-t^2} dt &\approx \sum_{i=0}^3 e^{-t_i^2}\Delta t\\ &= e^{-0}0.5 + e^{-0.5^2}0.5 + e^{-1^2}0.5 + e^{-1.5^2}0.5\\ &\approx 1.126 \end{align*}

Similar pages

See also