Elementary integral problems
Problem 1
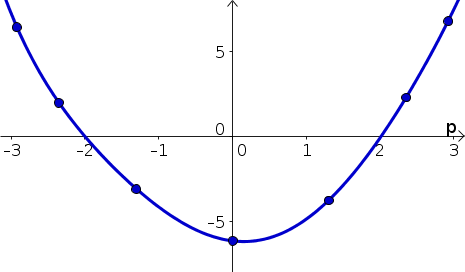
Below is a graph of the function $h(p)$. Let $H(p)=\int h(p) dp$ be the indefinite integral of $h(p)$.
- For what values of $p$ is $H(p)$
- increasing?
- decreasing?
- Use this information to sketch $H(p)$.
Problem 2
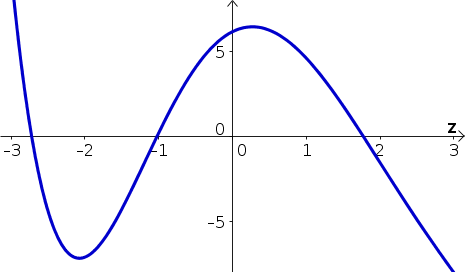
Below is a graph of the function $r(z)$. Let $R(z)=\int r(z) dz$ be the indefinite integral of $r(z)$.
- For what values of $z$ is $R(z)$
- increasing?
- decreasing?
- Use this information to sketch $R(z)$.
Problem 3
Calculate $$\int (3z^3-2/z^2-1)dz.$$
Problem 4
Find an antiderivative of $h(u)=\sqrt{u}-e^u$.
Problem 5
Calculate $$\int e^{-3t} dt.$$
Problem 6
Find an antiderivative of $g(t)= e^{-3t}$.
Problem 7
Solve the following pure-time differential equation. \begin{align*} \diff{m}{t} &= e^{-3t}\\ m(0) &= 1 \end{align*}
Problem 8
Solve the following pure-time differential equation. \begin{align*} \diff{q}{t} &= (1+4t)e^{2t^2+t-5}\\ q(0) &= 6 \end{align*}
Problem 9
Solve the following pure-time differential equation. \begin{align*} \diff{r}{t} &= 2t^3-6t^2+t-1\\ r(2) &= 3 \end{align*}
Problem 10
Evaluate $$\int_2^3 (1-x^2+x^{-1}) dx.$$
Problem 11
Calculate the average value of $f(z)=3z^2+7$ over the interval $[-1,2]$.
Problem 12
Find the area under graph of $g(x)=2e^{-x}$ over the interval $[-1, 0]$.
Problem 13
You are blowing up a balloon, increasing its volume. If $V(t)$ is the volume of the ballon at time $t$ seconds after you began blowing it up, then the volume is increasing according to \begin{align*} \diff{V}{t} = \sqrt{t}-\frac{t^2}{40}. \end{align*} If the balloon started at time $t=0$ completely deflated (i.e., with zero volume), solve this equation to determine the volume $V(t)$ at second $t$.
Problem 14
The price of an internet stock is changing according to the equation \begin{align*} \diff{p}{t} &= (2-t/2)e^{2t-t^2/4}, \end{align*} where $p(t)$ is its share price in dollars at time $t$, where $t$ is measured in years after the stock was made available (i.e., after its initial public offering). If the initial share prices was $p(0)=1$, solve this equation to determine the stock price $p(t)$ in year $t$. Give the share price (rounded to the nearest cent or 1/100 of a dollar) of the stock one year, four years, and ten years after the stock was made available.
Problem 15
Estimate the solution to the pure-time differential equation \begin{align*} \diff{h}{t} &= e^{-t^2}\\ h(0) &= 3 \end{align*} using the Forward Euler algorithm. Use a time step of $\Delta t = 0.5$ to estimates $h(2)$.
Problem 16
Estimate the definite integral \begin{align*} \int_0^2 e^{-t^2} dt \end{align*} using a left Riemann sum. Use a interval width of $\Delta t = 0.5$.
One you have worked on a few problems, you can compare your solutions to the ones we came up with.
Similar pages
- Solutions to elementary integral problems
- Area and definite integrals
- Developing intuition about the indefinite integral
- Basic integration formulas
- The simplest integration substitutions
- Integration substitutions
- Length of curves
- Numerical integration
- Averages and weighted averages
- Centers of mass (centroids)
- More similar pages