Vector line integral examples
Example 1
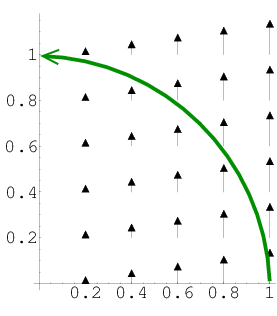
If a force is given by \begin{align*} \dlvf(x,y) = (0,x), \end{align*} compute the work done by the force field on a particle that moves along the curve $\dlc$ that is the counterclockwise quarter unit circle in the first quadrant. In the below picture, the curve $\dlc$ is plotted by the long green curved arrow. The vector field $\dlvf$ is represented by the vertical black arrows.
Solution: First, can you see what the sign of the integral should be? Notice that curve and the vector field are mostly going in the same direction. The tangent vector to the curve and the vector field always make an angle less that $\pi/2$. So, their dot product must be positive everywhere along the curve, which means the integral must be positive.
The first step to computing the integral is to parametrize the curve $\dlc$. We'll parametrize it by \begin{align*} \dllp(t) = (\cos t, \sin t), \quad 0 \le t \le \frac{\pi}{2}. \end{align*} so that the derivative is \begin{align*} \dllp'(t) = (-\sin t, \cos t). \end{align*} The work is the line integral \begin{align*} \dlint &= \plint{0}{\pi/2}{\dlvf}{\dllp}\\ &= \int_0^{\pi/2} \dlvf(\cos t, \sin t) \cdot (-\sin t, \cos t) dt\\ &= \int_0^{\pi/2} (0, \cos t) \cdot (-\sin t, \cos t) dt\\ &= \int_0^{\pi/2} \cos^2 t\, dt\\ &= \int_0^{\pi/2} \frac{1}{2} (1 + \cos 2t) dt\\ &= \frac{1}{2} \left.\left(t + \frac{\sin 2t}{2}\right) \right|_0^{\pi/2} = \frac{1}{2} \left(\frac{\pi}{2} - 0\right) = \frac{\pi}{4}. \end{align*}
It's a good thing the answer is positive, so it agrees with what we read off the picture.
Example 2
The integral $\dlint$ does not depend on parameterization, as long as we parametrize $C$ to with the counter-clockwise orientation. To see this, calculate the integral of example 1 using the parametrization \begin{align*} \adllp(t) = (\sqrt{1-t^2},t), \qquad 0 \le t \le 1. \end{align*}
Solution: Since \begin{align*} \adllp'(t) = \left(\frac{-t}{\sqrt{1-t^2}}, 1\right), \end{align*} the work is \begin{align*} \dlint &= \plint{0}{1}{\dlvf}{\adllp}\\ &=\int_0^1 \dlvf(\sqrt{1-t^2},t) \cdot \left(\frac{-t}{\sqrt{1-t^2}}, 1\right) dt\\ &= \int_0^1 (0, \sqrt{1-t^2})\cdot \left(\frac{-t}{\sqrt{1-t^2}}, 1\right) dt\\ &= \int_0^1 \sqrt{1-t^2} dt. \end{align*} To complete this integral, use the $u$-substitution $t=\sin u$, so that $dt = \cos u \, du$. Since $t$ goes from 0 to 1, $u$ must go from 0 to $\pi/2$. Thus, the integral becomes \begin{align*} \dlint &= \int_0^{\pi/2} \sqrt{1-\sin^2u} \cos u \, du\\ &= \int_0^{\pi/2} \sqrt{\cos^2 u} \cos u \, du\\ &= \int_0^{\pi/2} \cos^2 u \, du. \end{align*} This is exactly the same integral we had for Example 1 (if replace $t$ with $u$ in the third line from the bottom of Example 1). So we immediately see that the work is, again, $\pi/4$.
Example 3
The integral $\dlint$ does depend on the orientation of $C$. If we reverse its orientation to clockwise, we should switch the sign of the integral. Verify this by calculating the integral of the same vector field $\dlvf$ as example 1, but on the clockwise quarter unit parametrized by $\sadllp(t) = (\sin t, \cos t)$ for $0 \le t \le \pi/2$.
Solution: Since \begin{align*} \dlvf(\sadllp(t)) & = (0,\sin t)\\ \sadllp'(t) &= (\cos t, -\sin t), \end{align*} the line integral is \begin{align*} \dlint &= \plint{0}{\pi/2}{\dlvf}{\sadllp}\\ &= \int_0^{\pi/2} (0,\sin t) \cdot (\cos t, -\sin t) dt \\ &= \int_0^{\pi/2} -\sin^2t dt\\ &= \int_0^{\pi/2} -\frac{1}{2}(1-\cos 2t)dt\\ &= -\frac{1}{2} \left.\left(t - \frac{\sin 2t}{2}\right) \right|_0^{\pi/2} = -\frac{1}{2} \left(\frac{\pi}{2} + 0\right) = -\frac{\pi}{4}. \end{align*}
As we knew it had to, the line integral changed signs. Now the integral is negative, as the curve tends to move in the opposite direction of the vector field.
Example 4
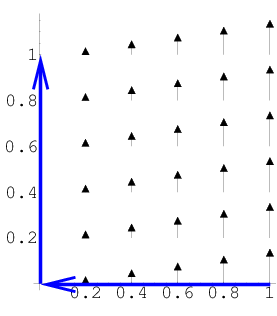
The line integral does, in general depend on the path. The path for Example 1 started at (1,0) and ended at (0,1). What is the integral \begin{align*} \dlint \end{align*} if $\dlc$ is the following different path (shown in blue) from (1,0) to (0,1)?
Solution: We can find this answer without doing any computations.
The first part of the path is moving left along the $x$-axis. In that case, the path is orthogonal to the vector field, which points up. Therefore, the dot product between the vector field and the tangent vector is always zero. The force does no work on the particle during this first segment.
The second part of the path is moving straight up along the $y$-axis. Along the $y$-axis, $x=0$, so that $\vc{F}(x,y)=(0,x)=(0,0)$. The vector field is zero, and the integral of zero is zero. We can conclude that \begin{align*} \dlint = 0. \end{align*}
Thread navigation
Multivariable calculus
Math 2374
Notation systems
Similar pages
- Introduction to a line integral of a vector field
- Alternate notation for vector line integrals
- Line integrals as circulation
- Introduction to a line integral of a scalar-valued function
- Line integrals are independent of parametrization
- Examples of scalar line integrals
- The idea behind Green's theorem
- The integrals of multivariable calculus
- Vector field overview
- Vector fields as fluid flow
- More similar pages