Applet: A rotating sphere indicating the presence of curl
Applet loading
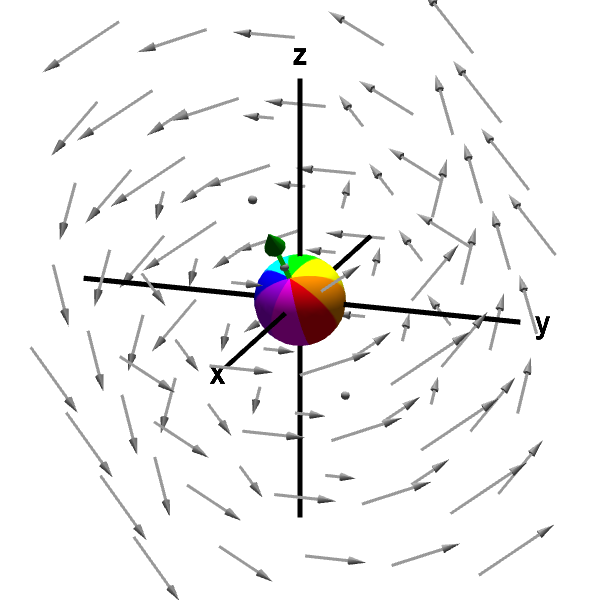
The rotation of the sphere, with its center fixed at a point (originally the origin), indicates the presence of nonzero curl at that point. The curl at that point is represented by the green arrow. The length of the curl vector indicates the rotation speed. The direction of the curl vector is determined by the rotation direction using the “right hand rule”: curl finger of right hand in direction of rotation and your thumb will indicate the direction of the curl vector. (You can rotate the graph with the mouse to see the green arrow better.)
This vector field is $\dlvf(x,y,z)= (-y,x-z,y).$ Its curl is \begin{align*} \curl \dlvf(x,y,z) &= \left(\pdiff{}{y}y-\pdiff{}{z}(x-z), \pdiff{}{z}(-y)- \pdiff{}{x}y, \pdiff{}{x}(x-z) - \pdiff{}{y}(-y) \right)\\ &=(2,0,2), \end{align*} which is a constant independent of point $(x,y,z)$ and always points at an angle halfway between the positive $x$ and $z$ axes. Since the curl is constant independent of the point $(x,y,z)$, the sphere spins in the same direction and with the same speed and the green arrow representing the curl is the same, no matter where the sphere is moved. (You can move the sphere by dragging it with the mouse.)
Applet links
This applet is found in the pages
General information about three.js applets
The applet was made using three.js and requires Javascript as well as a browser that supports WebGL. For most three.js applets, you can drag with the mouse to rotate the view, drag with the right button to pan, and zoom in/out with the mouse wheel. Many applets contain points that you can drag to change values of variables.